Частная школа. 9 класс

О Г Л А В Л Е Н И Е Вернуться к списку тем учебника

Алгебра 9 класс. УМК Макарычев и др. Онлайн-учебник 2017. Глава 1. КВАДРАТИЧНАЯ ФУНКЦИЯ. § 4. Степенная функция. Корень n–й степени (Функция у = хⁿ. Корень n–й степени. Дробно-линейная функция и её график. Степень с рациональным показателем. Дополнительные упражнения к главе I).  Электронная версия.

 

§ 4. Степенная функция. Корень n–й степени

8. Функция у = хⁿ.

Рассмотрим функцию, заданную формулой у = хⁿ, где х – независимая переменная, а n – натуральное число. Такую функцию называют степенной функцией с натуральным показателем.

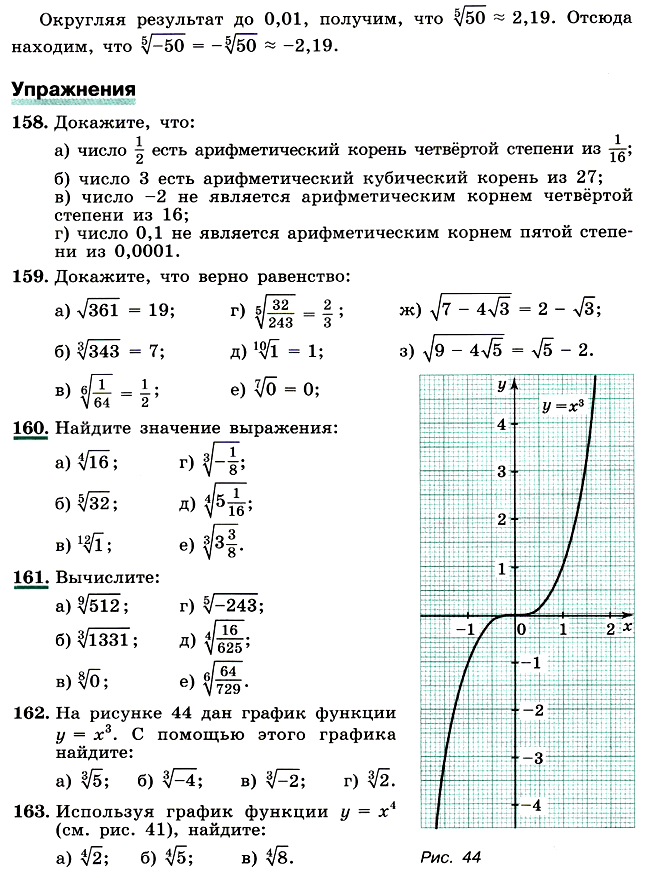
Степенные функции при n = 1, 2 и 3, т. е. функции у = х, у = x² и у = х³, вы уже рассматривали. Их свойства и графики вам известны.

Выясним теперь свойства степенной функции и особенности её графика при любом натуральном n.

Выражение хⁿ, где n – натуральное число, имеет смысл при любом х. Поэтому областью определения степенной функции с натуральным показателем является множество всех действительных чисел.

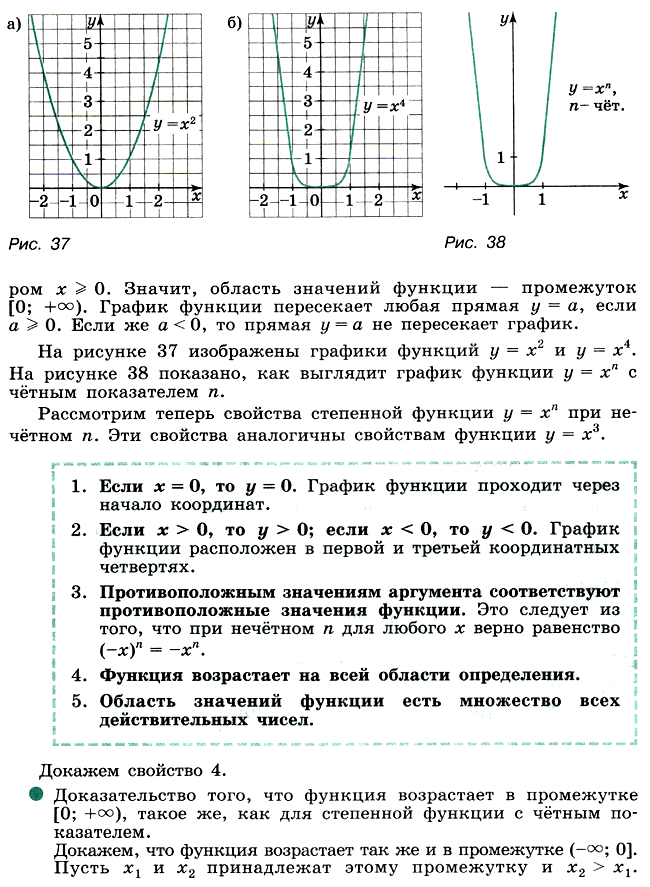
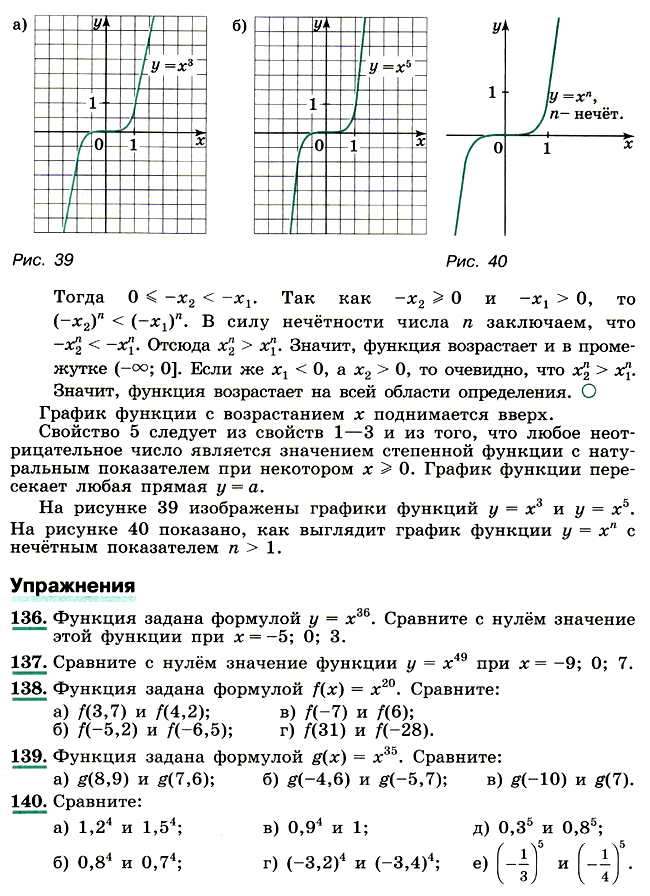
Сначала рассмотрим случай, когда показатель n – чётное число. Свойства функции у = хⁿ при чётном n аналогичны свойствам функции у = x².

Если х = 0, то у = 0. График функции проходит через начало координат. Если х ≠ 0, то у > 0. Это следует из того, что чётная степень как положительного, так и отрицательного числа положительна. График функции расположен в первой и второй координатных четвертях. Противоположным значениям аргумента соответствуют равные значения функции. Это следует из того, что при чётном п равенство (–х)n = хn верно при любых значениях x. Функция возрастает в промежутке [0; +∞) и убывает в промежутке (–∞; 0]. Область значений функции есть множество неотрицательных чисел.

---

 

9. Корень n-й степени.

---

 

 

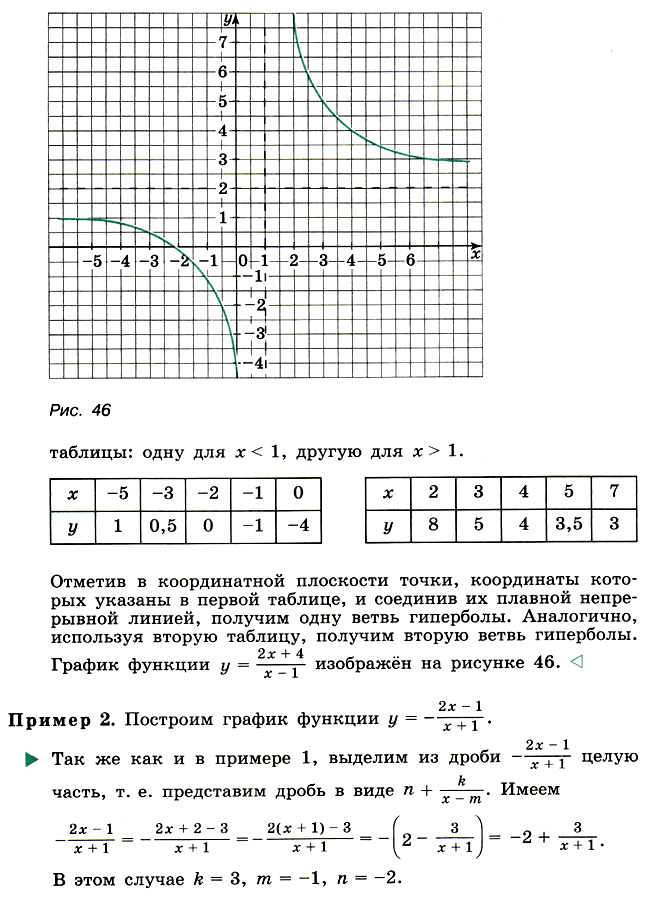
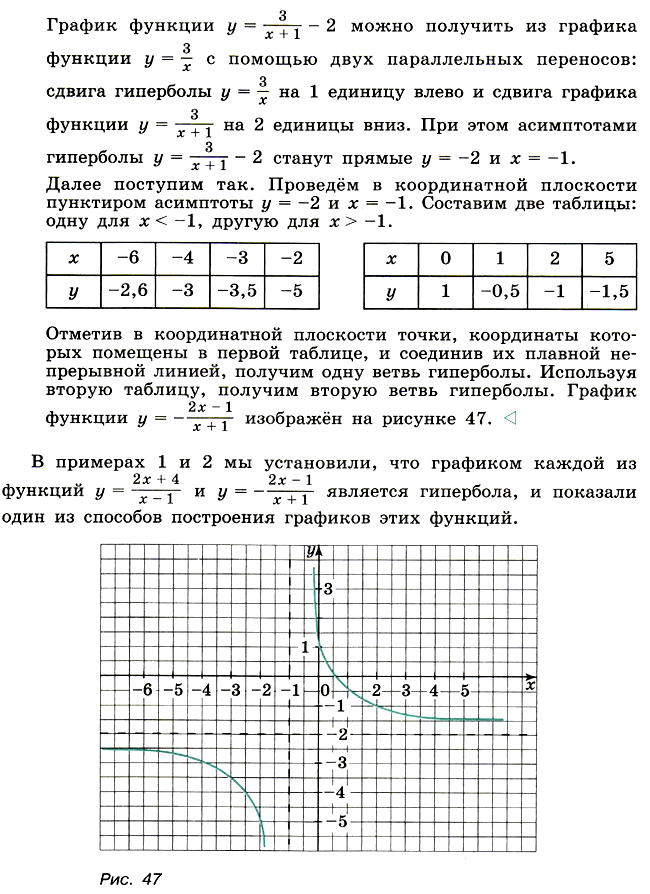
10. Дробно-линейная функция и её график.

---

 

 

11. Степень с рациональным показателем).

---

 

Дополнительные упражнения к главе I.

---

 

 

О Г Л А В Л Е Н И Е Вернуться к списку тем учебника

---

Алгебра 9 класс. УМК Макарычев и др. Онлайн-учебник. Глава 1. КВАДРАТИЧНАЯ ФУНКЦИЯ. § 4. Степенная функция. Корень n–й степени (Функция у = хⁿ. Корень n–й степени. Дробно-линейная функция и её график. Степень с рациональным показателем. Дополнительные упражнения к главе I). Электронная версия.