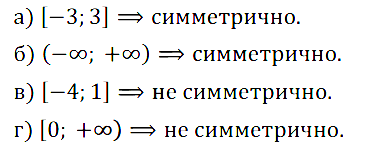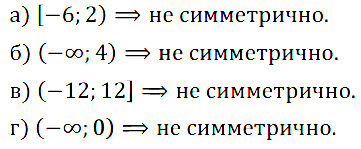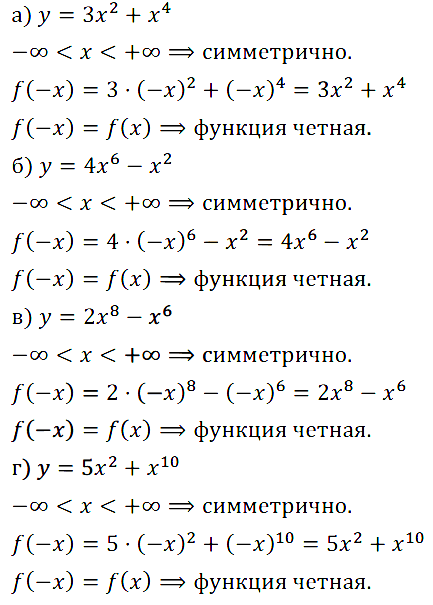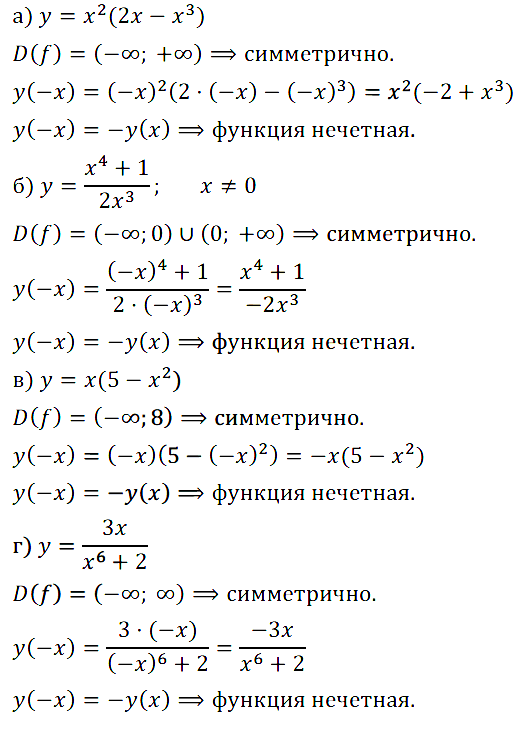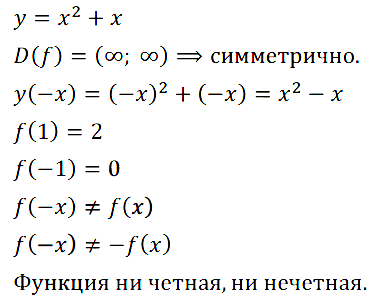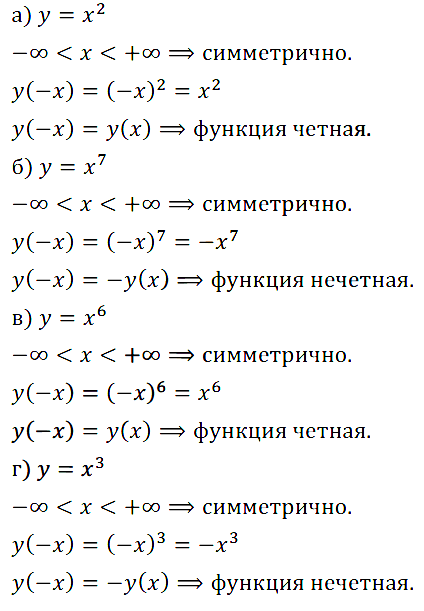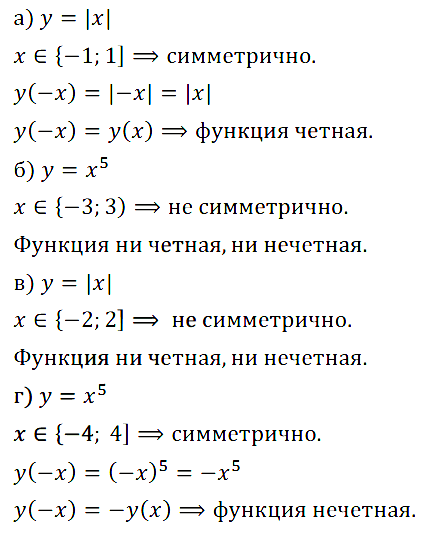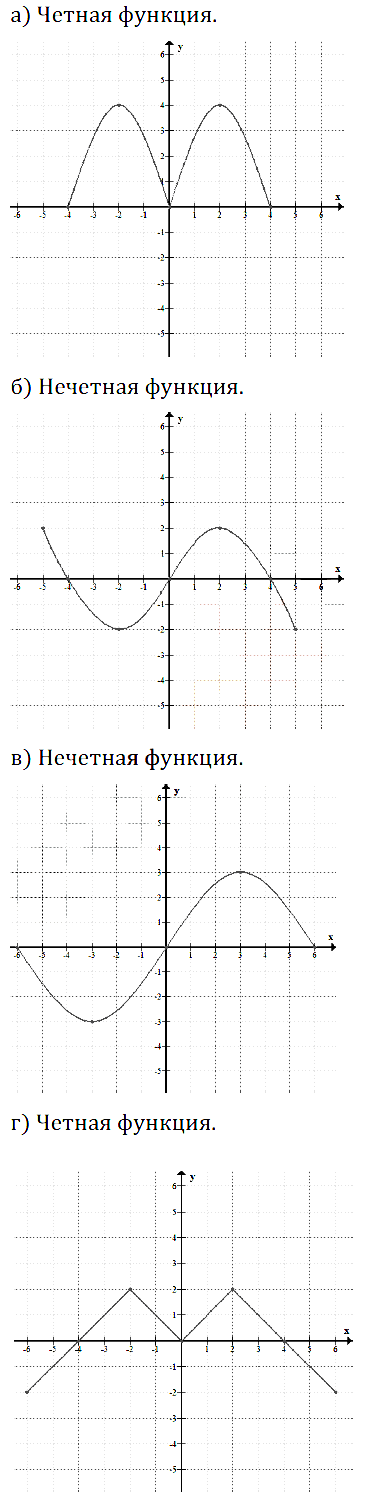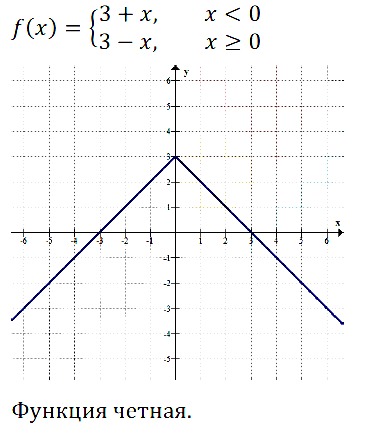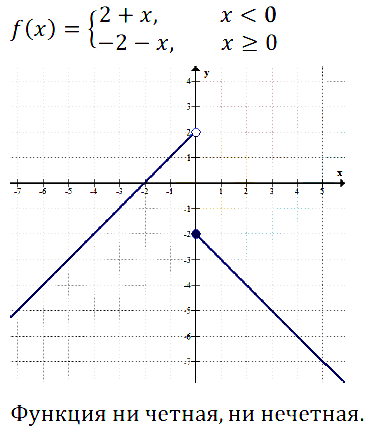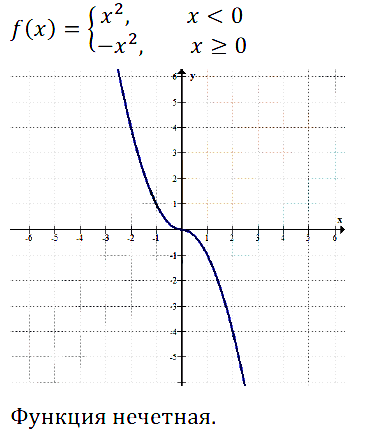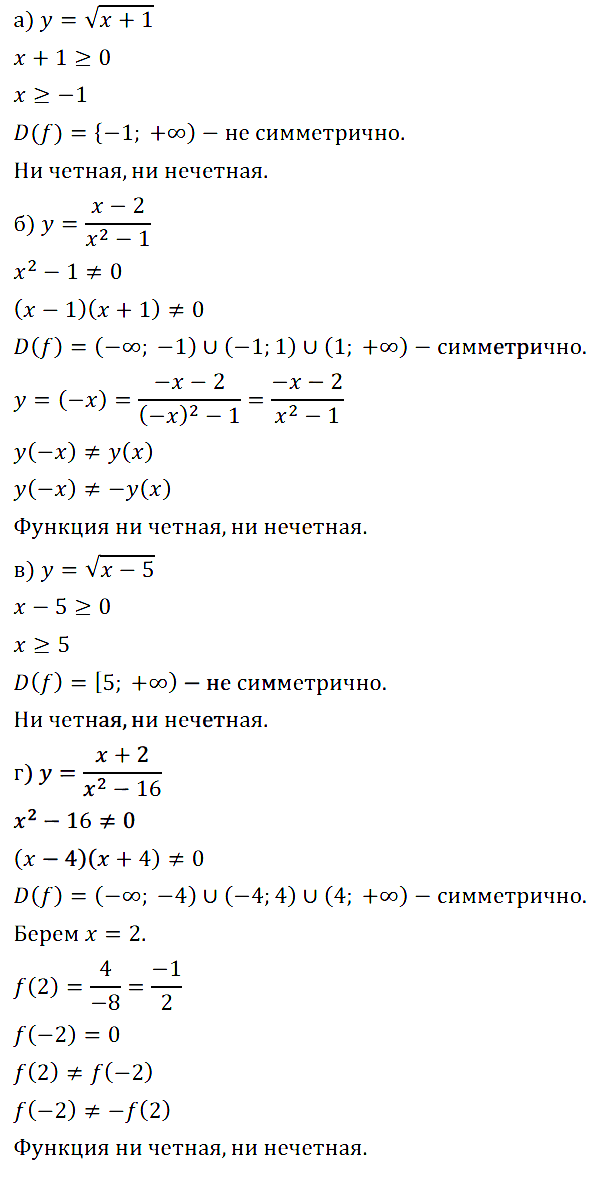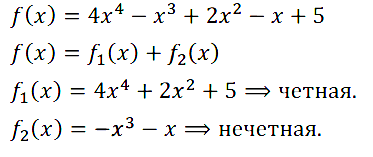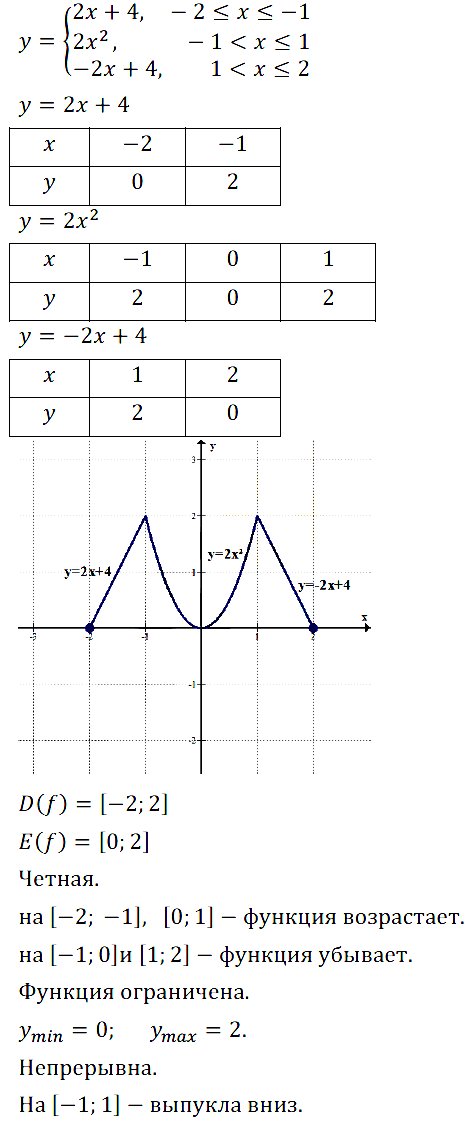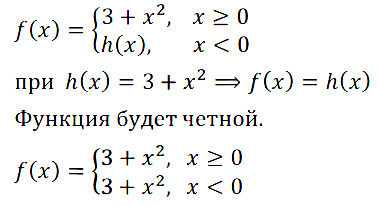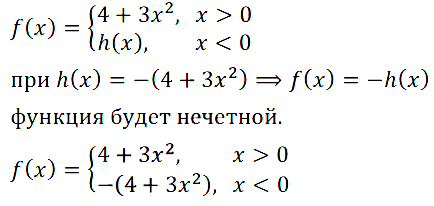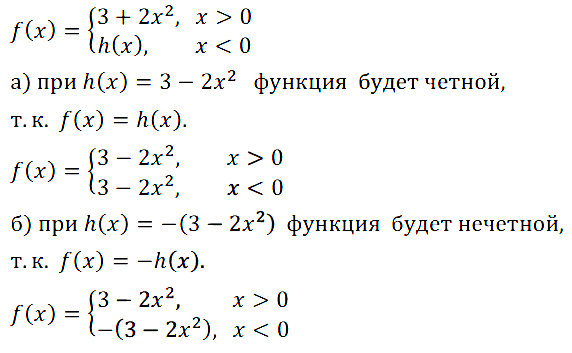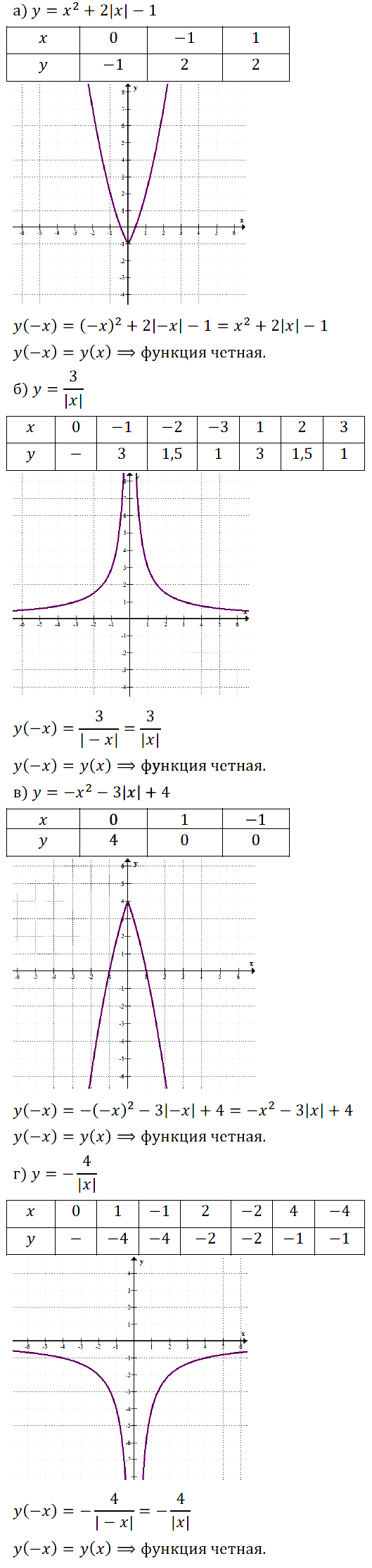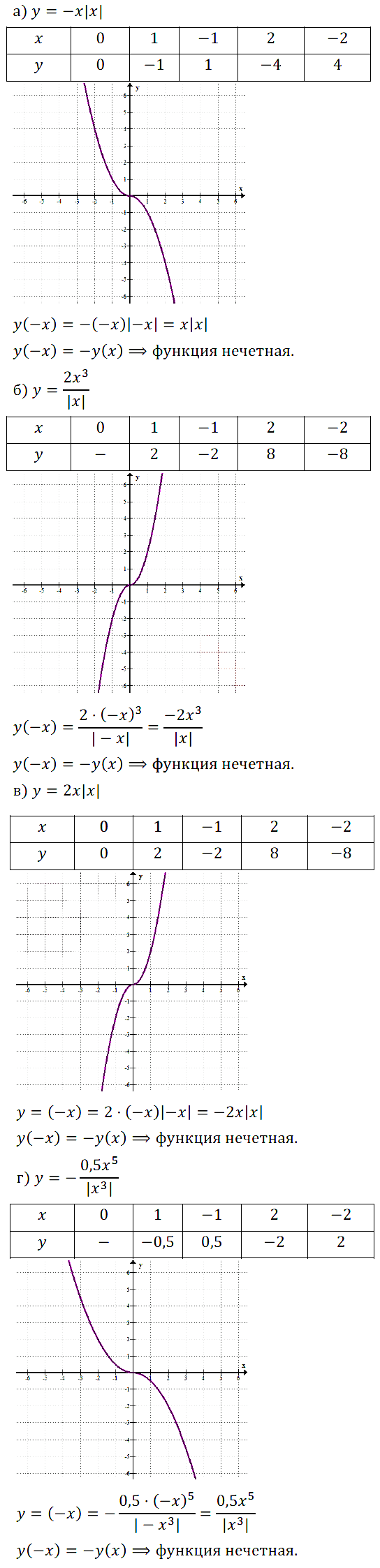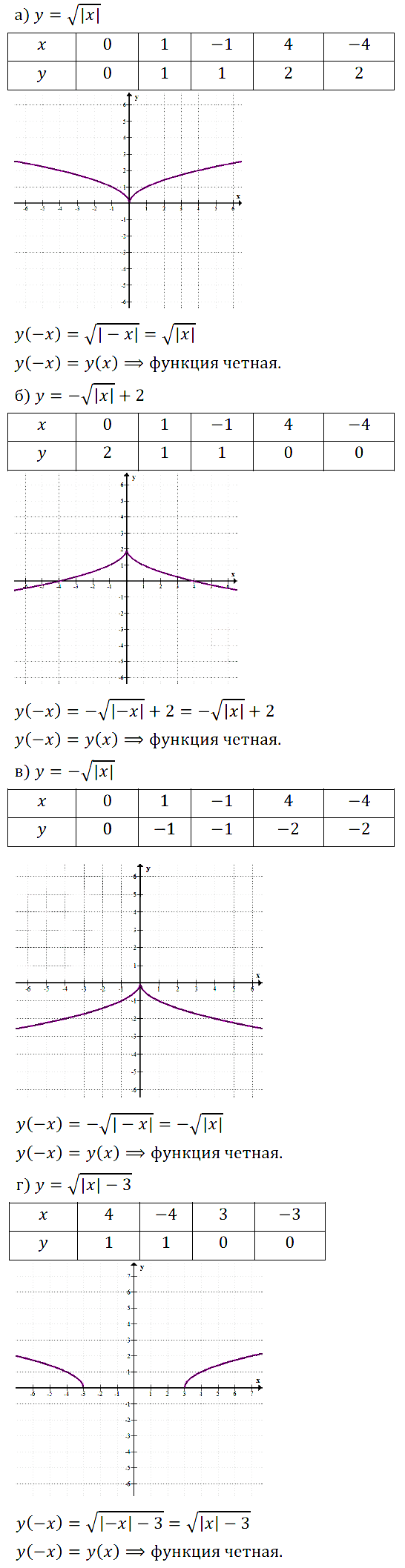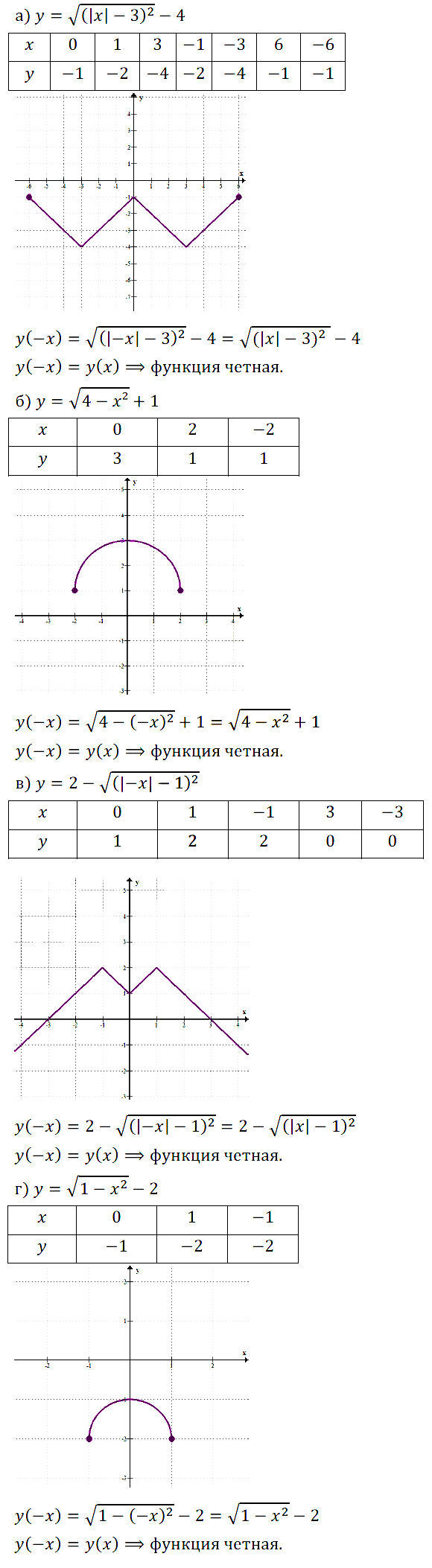Частная школа. 9 класс

Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ОТВЕТЫ на упражнения 11.1 — 11.34. § 11. Чётные и нечётные функции. ГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИ.

ОГЛАВЛЕНИЕ Вернуться к списку тем учебника

 

Алгебра 9 класс (Мордкович)
Упражнения №№ 11.1 — 11.34

Нажмите на спойлер, чтобы посмотреть ответ на задание.

ГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИ

§ 11. Чётные и нечётные функции

Является ли симметричным заданное множество:

Задание № 11.1.  a) [–3; 3];  б) (–∞; +∞);  в) [–4; 1];   г) [0; +∞)?

Задание № 11.2. а) [–6; 2);   б) (– ∞;4);   в) (–12; 12];   г)(–∞; 0)?

Задание № 11.3.  Докажите, что функция является чётной:
а) у = 3x² + х⁴;  б) у = 4x⁶ – x²;  в) у = 2x⁸ – x⁶;  г) у = 5x² + x¹⁰.

Задание № 11.4. Докажите, что функция является нечётной:
а) у = x²(2x – x³);   б) у = (х⁴ + 1)/2х³;   в) у = x(5 – x²);   г) у = 3х/(х⁶ + 2).

Задание № 11.5.  Докажите, что функция у = x² + х не является ни чётной, ни нечётной.

Исследуйте на чётность функцию:
Задание № 11.6. а) у = x²; б) у = х⁷; в) у = х⁶; г) у = х³.

Задание № 11.7.

Задание № 11.8.

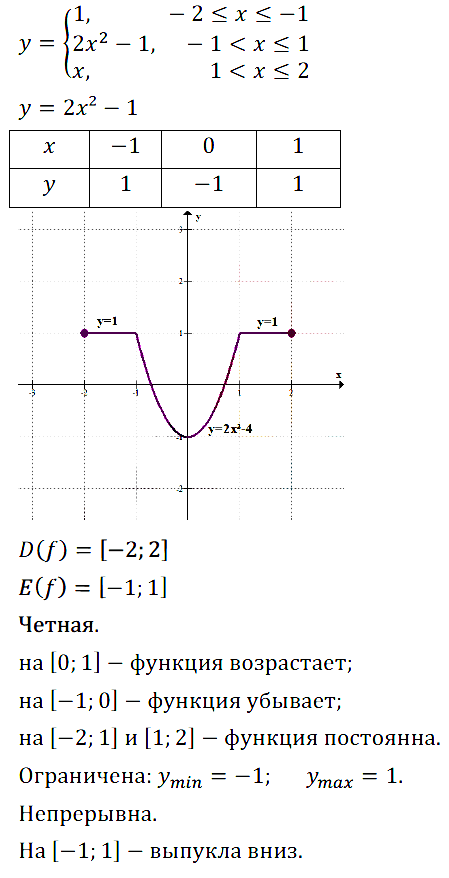
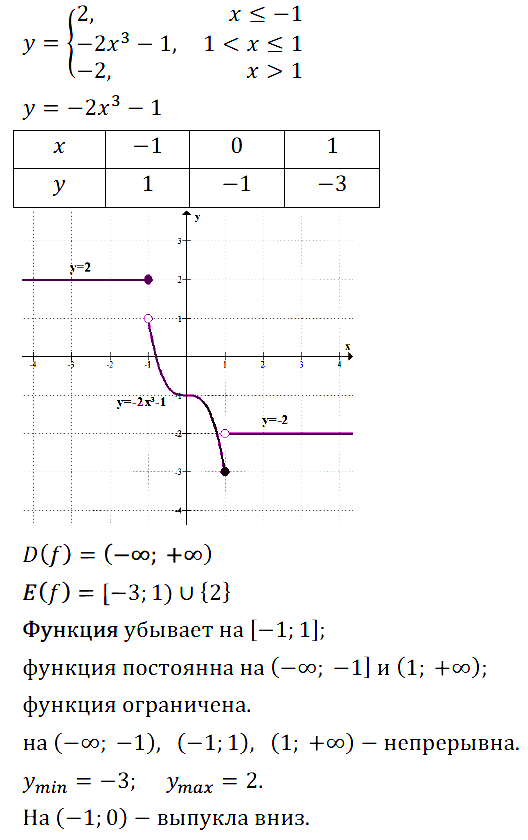
Исследуйте на чётность функцию, график которой изображён:
Задание № 11.9.  а) На рис. 43;   б) на рис. 44;   в) на рис. 45;   г) на рис. 46.

Задание № 11.10.  а) На рис.47;  б) на рис.48;  в) на рис. 49;  г) на рис. 50.

Задание № 11.11. На рисунке построена ветвь графика функции у = f(x). Постройте весь график этой функции, если известно, что:
а) у = f(x) — чётная функция (рис. 51);
б) у = f{x) — нечётная функция (рис. 52);
в) у = f(x) — нечётная функция (рис. 53);
г) у = f(x) — чётная функция (рис. 54).

Задание № 11.12. а) Известно, что функция у = f(x) — чётная и возрастает при х > 0. Определите характер монотонности функции при х < 0.
б) Известно, что функция у = f(x) — чётная и убывает при х > 0. Определите характер монотонности функции при х < 0.
в) Известно, что функция у = f(x) — нечётная и возрастает при х > 0. Определите характер монотонности функции при х < 0.
г) Известно, что функция у = f(x) — нечётная и убывает при х > 0. Определите характер монотонности функции при х < 0.

Задание № 11.13. Известно, что функция у = f(x) — чётная и ограничена сверху при х > 0. Можно ли утверждать, что она при х < 0: а) ограничена сверху; б) ограничена снизу?

Задание № 11.14. Известно, что функция у = f(x) — нечётная и ограничена снизу при х > 0. Можно ли утверждать, что она при х < 0: а) ограничена сверху; б) ограничена снизу?

Задание № 11.15. Известно, что функция у = f(x) — нечётная и ограничена сверху при х > 0. Можно ли утверждать, что она при х < 0: а) ограничена сверху; б) ограничена снизу?

Задание № 11.16. Известно, что функция у = f(x) — чётная и ограничена снизу при х > 0. Можно ли утверждать, что она при х < 0: а) ограничена сверху; б) ограничена снизу?

Задание № 11.17.

Задание № 11.18.

Задание № 11.19.

Задание № 11.20.

Задание № 11.21.

Задание № 11.22.

Задание № 11.23.

Задание № 11.24.

Задание № 11.25.

Задание № 11.26. Функции у = f(x) и у = g(x) определены на множестве всех действительных чисел. Является ли функция у = h(х) чётной или нечётной, если:
а) h(x) = f{x) • g²(x), у = f(x) — чётная функция, у = g(x) — нечётная функция;
б) h(x) = f(x) – g(x), у = f(x) и y = g(х) — чётные функции;
в) h(x) = f(x) + g(x), у = f(x) и у = g(x) — нечётные функции;
г) h(x) = f(x) • g(x), у = f(x) и y = g(x) — нечётные функции?

Задание № 11.27. Дана функция у = f(х), где f(x) = { 3 + x², если x ≥ 0; { h(x), если x < 0.
Задайте h(x) так, чтобы функция у = f(x) являлась чётной.

Задание № 11.28.

Задание № 11.29.

Задание № 11.30.

Задание № 11.31.

Задание № 11.32.

Задание № 11.33.

Задание № 11.34.

 

ОГЛАВЛЕНИЕ Вернуться к списку тем учебника

 

---

Вы смотрели: ГДЗ Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИ. § 11. Чётные и нечётные функции. ОТВЕТЫ на задачи 11.1 — 11.34.