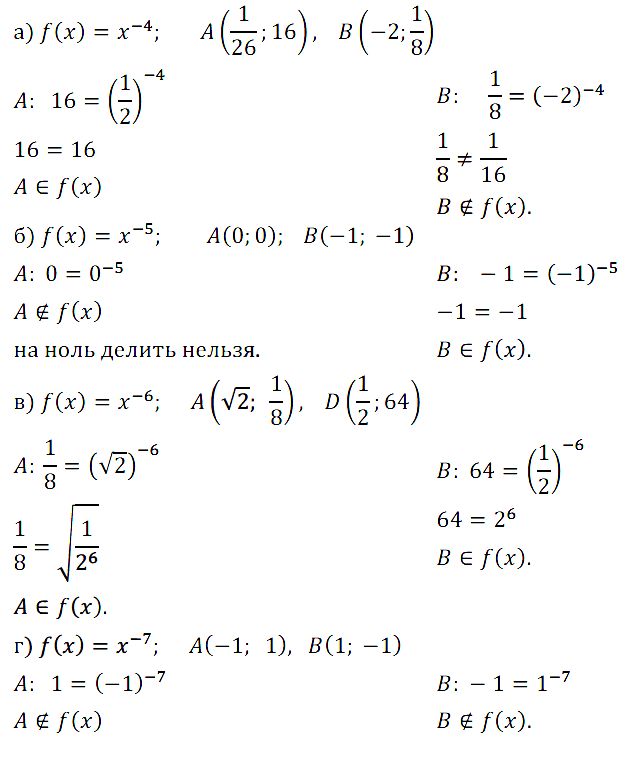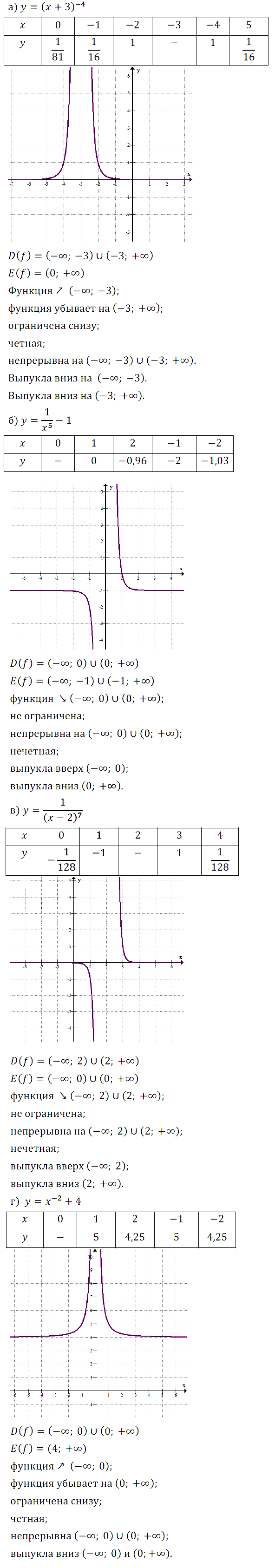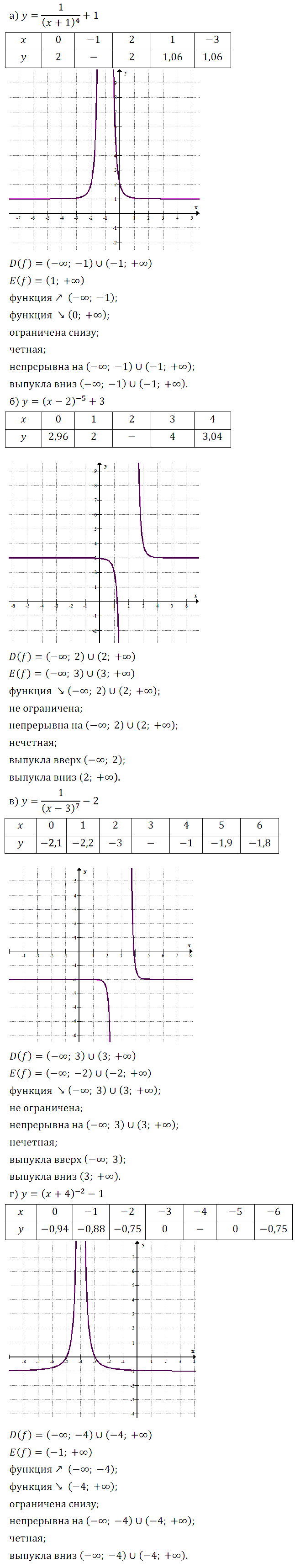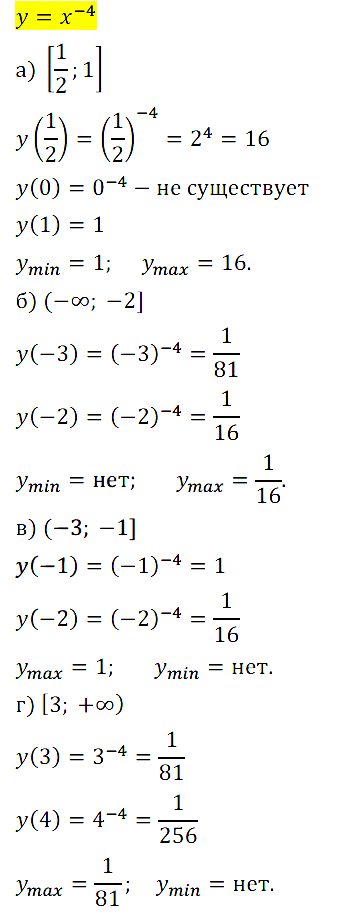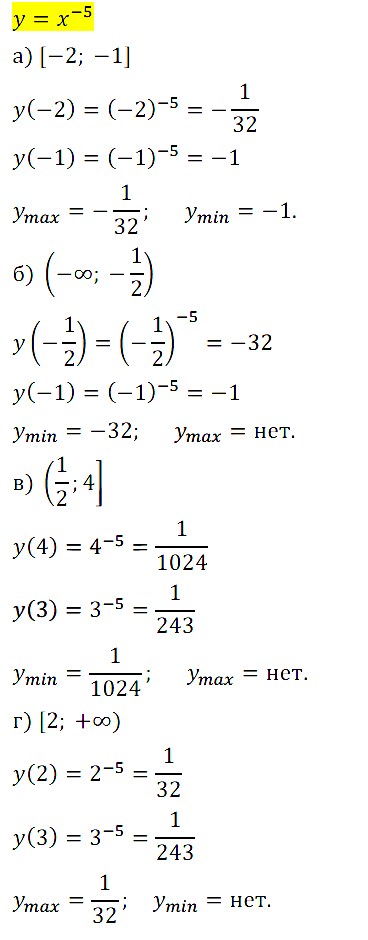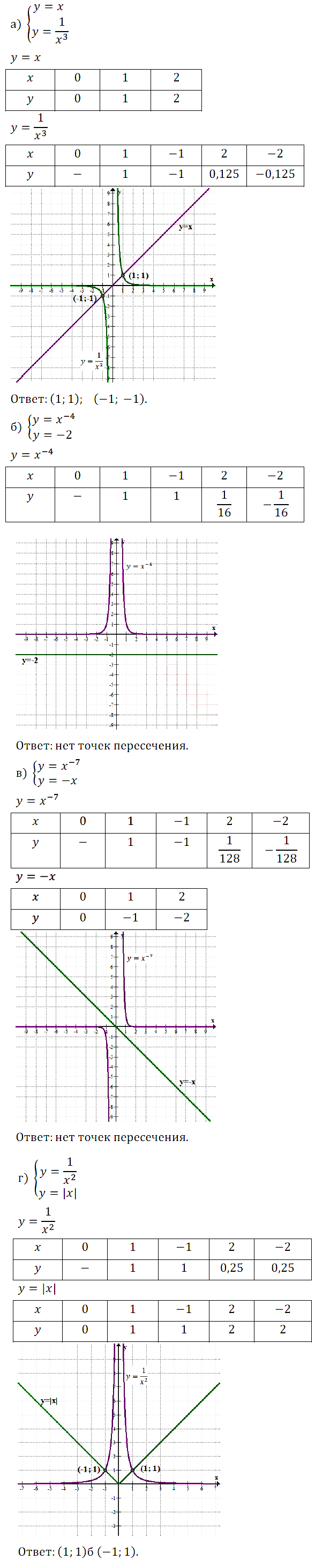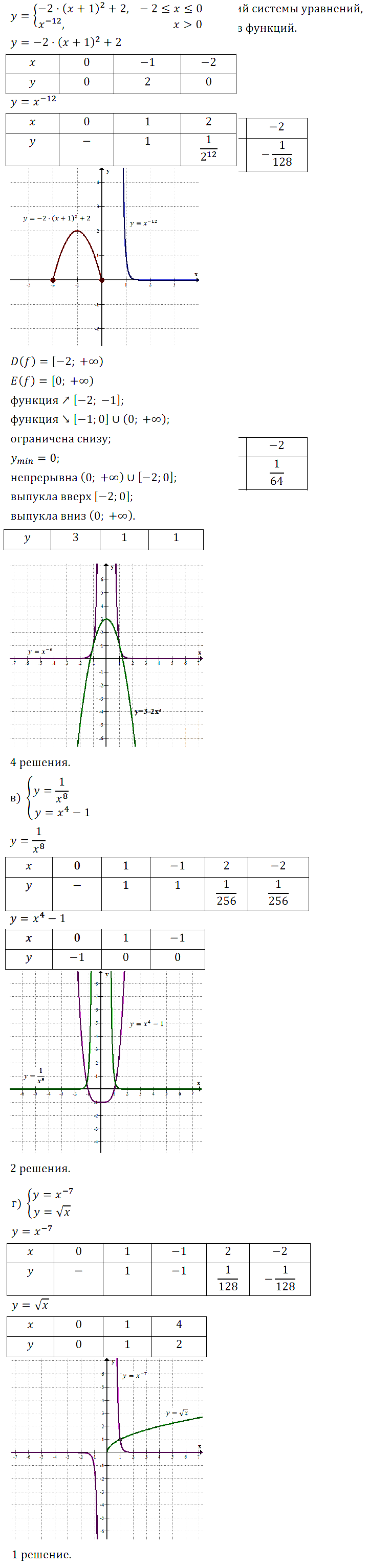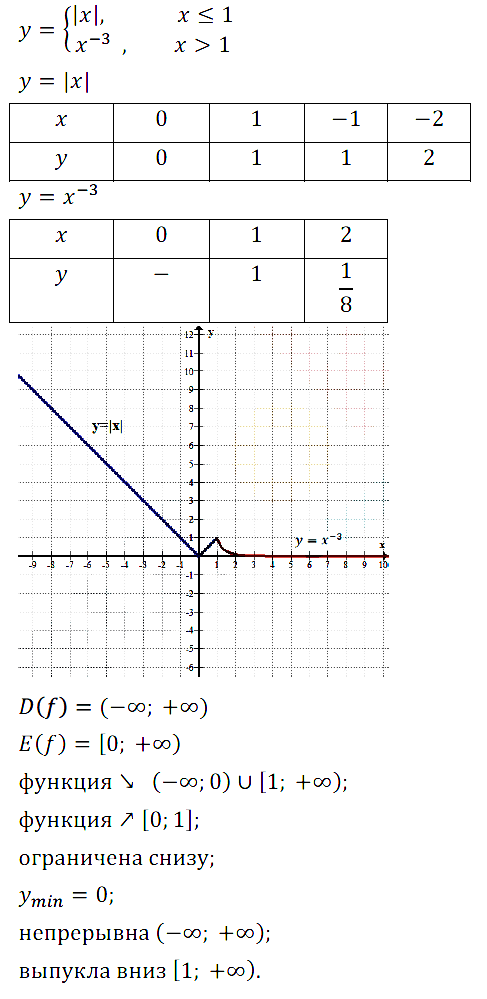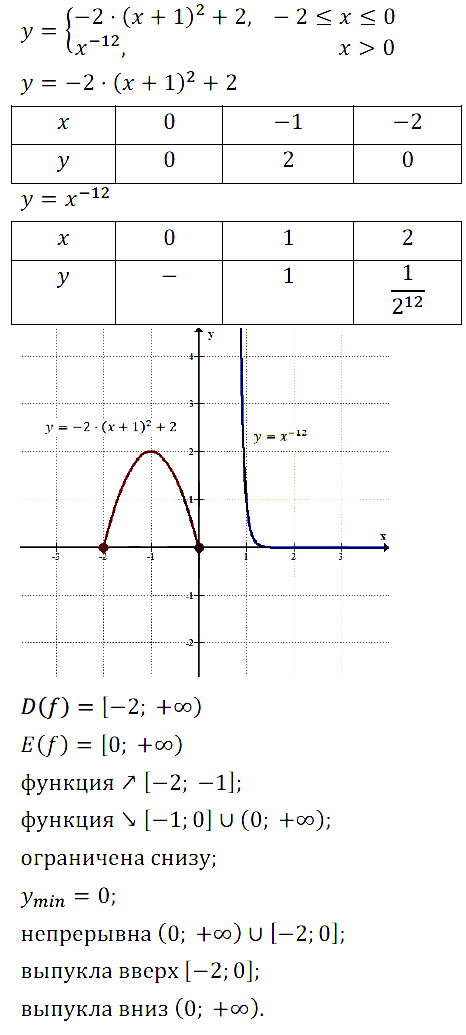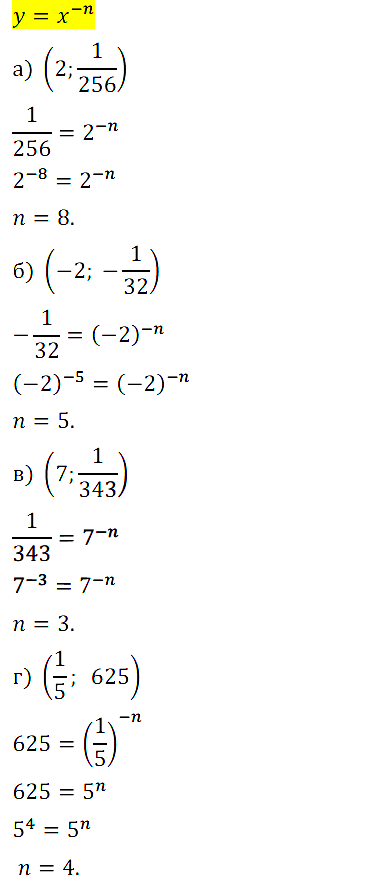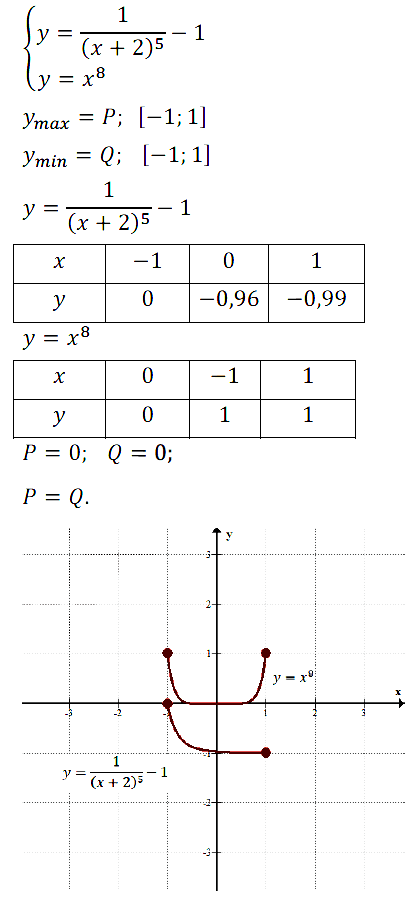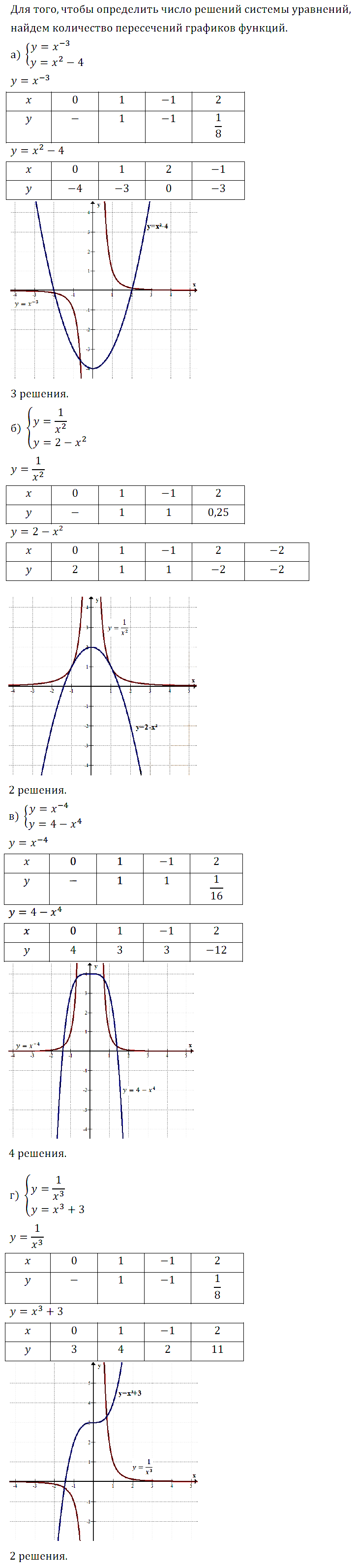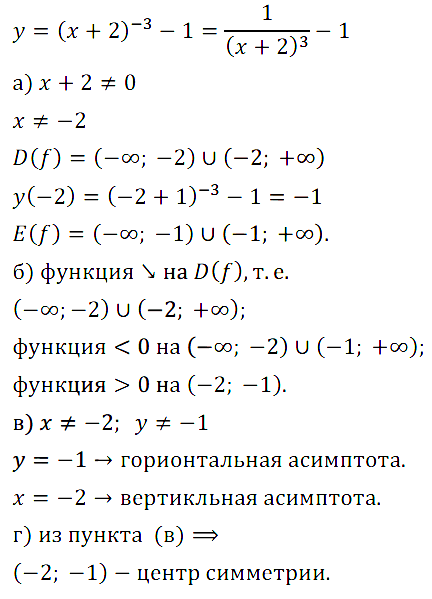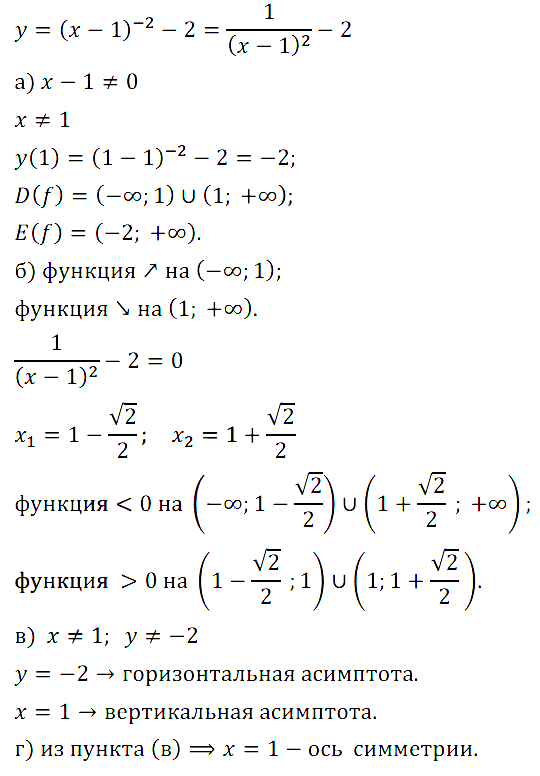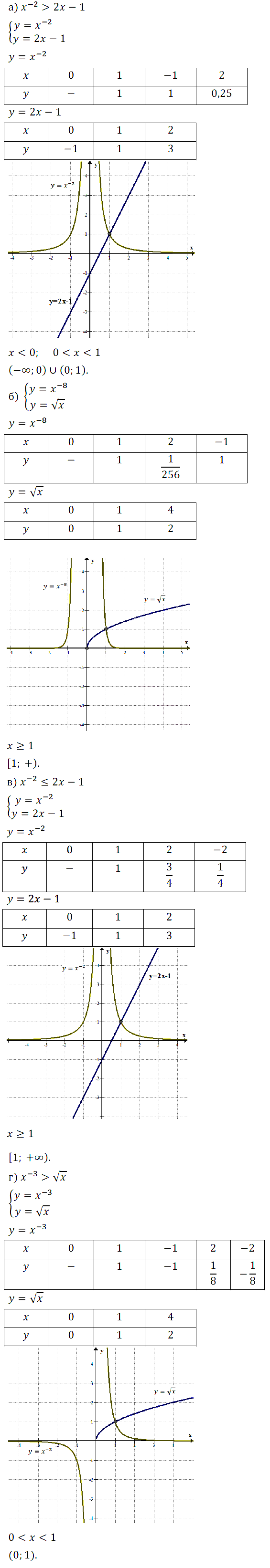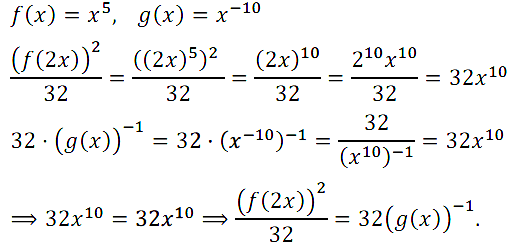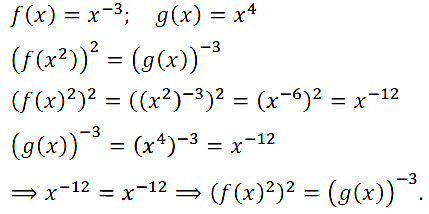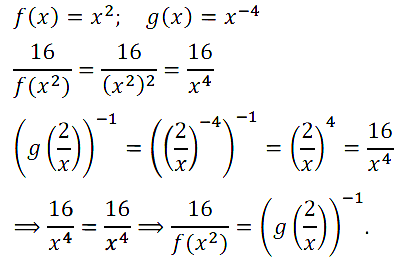Частная школа. 9 класс

Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ОТВЕТЫ на упражнения 13.1 — 13.25. § 13. Функции у = х^–n (n ∈ N), их свойства и графики. ГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИ.

ОГЛАВЛЕНИЕ Вернуться к списку тем учебника

 

Алгебра 9 класс (Мордкович)
Упражнения №№ 13.1 — 13.25

Нажмите на спойлер, чтобы посмотреть ответ на задание.

ГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИ

§ 13. Функции у = х^–n (n ∈ N), их свойства и графики

Задание № 13.1. Какая из точек А, В принадлежит графику функции у = f(x), если:
а) f(x) = х^–4, А(1/2; 16), В(–2; 1/8);
б) f(x) = х^–5, А(0; 0), В(–1; –1);
в) f(х) = х^–6, A(√2; 1/8), В(1/2; 64);
г) f(х) = х^–7, А(–1; 1), В(1; –1)?

Постройте и прочитайте график функции:
Задание № 13.2. а) y = 1/x⁴;   б) y = x^–3;   в) y = x^–8;   г) y = 1/x⁵.

Задание № 13.3. а) у = (х + 3)^–4;  б) y = 1/x⁵ – 1;   в) y = 1/(x – 2)⁷;   г) y = x^–2 + 4.

Задание № 13.4. а) y = 1/(x + 1)⁴ + 1; б) y = (x – 2)^–5 + 3; в) y = 1/(x – 3)⁷ – 2; г) y = (x + 4)^–2 – 1.

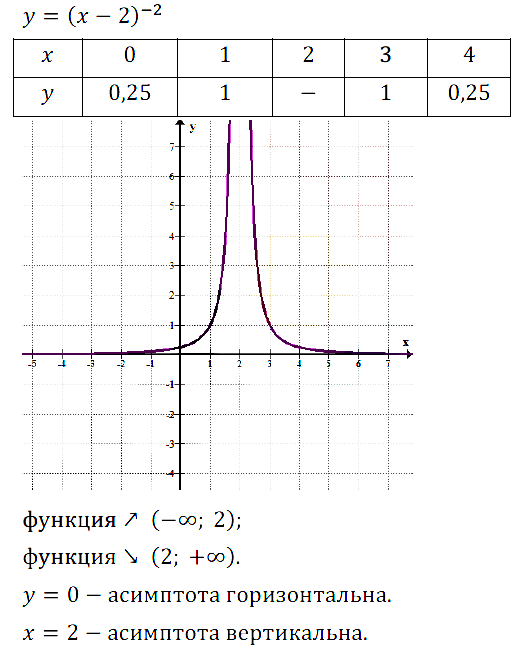
Задание № 13.5. Постройте график функции у = (х – 2)^–2. Найдите промежутки убывания и возрастания функции. Составьте уравнения горизонтальной и вертикальной асимптот.

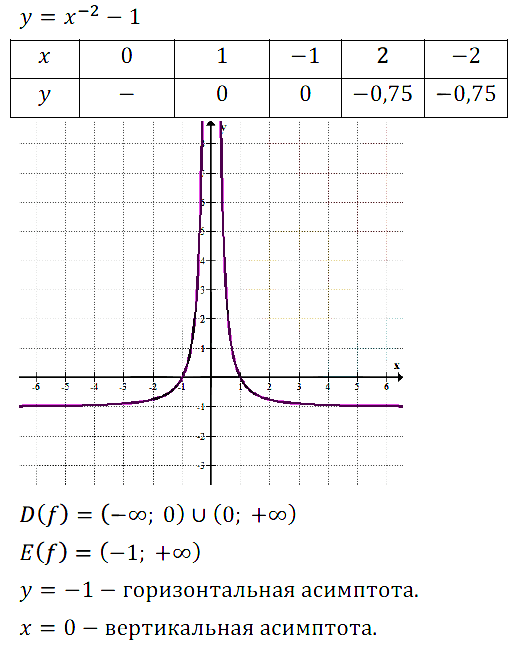
Задание № 13.6. Постройте график функции у = х^–2 – 1. Найдите область значений функции. Составьте уравнения горизонтальной и вертикальной асимптот.

Задание № 13.7. Найдите наименьшее и наибольшее значения функции у = х^–4:
а) на отрезке [1/2; 1]; б) на луче (–∞; –2]; в) на полуинтервале (–3; –1]; г) на луче [3; + ∞).

Задание № 13.8. Найдите наименьшее и наибольшее значения функции у = х^–5:
а) на отрезке [–2; –1]; б) на луче (–∞; –1/2]; в) на полуинтервале (1/2; 4]; г) на луче [2; +∞).

Задание № 13.9. Найдите точки пересечения графиков функций:
а) y = х и у = 1/x³;  б) у = х^–4 и у = –2;  в) у = х^–7 и у = –х;  г) у = 1/x² и y = |x|.

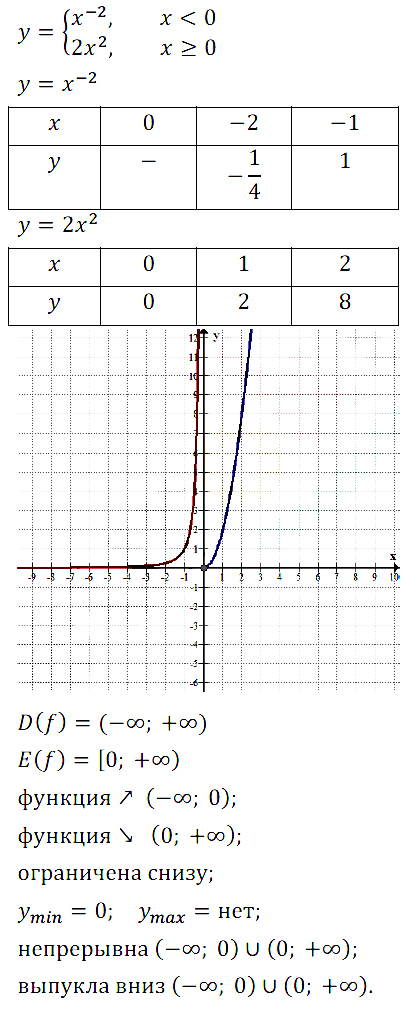
Задание № 13.10.

Задание № 13.11.

Задание № 13.12.

Задание № 13.13.

Задание № 13.14.

Задание № 13.15. Чему равно n, если известно, что график степенной функции у = х^–n проходит через заданную точку: а) (2; 1/256); б) (–2; –1/32); в) (7; 1/343); г) (1/5; 625) ?

Задание № 13.16. Исследуйте степенную функцию у = х^–n на чётность и ограниченность, если известно, что её график проходит через заданную точку: а) (–1; 1); б) (–1; –1); в) (1; 1); г) (1; –1).

Задание № 13.17. Пусть Р — наибольшее значение функции у = 1/(x + 2)⁵ – 1 на отрезке [–1; 1], a Q — наименьшее значение функции у = х⁸ на отрезке [–1; 1]. Что больше: Р или Q? Сделайте графическую иллюстрацию.

Задание № 13.18.

Задание № 13.19. Не выполняя построения графика функции у = (х + 2)^–3 – 1, укажите:
а) область определения и область значений функции;
б) промежутки монотонности и промежутки знакопостоянства функции;
в) уравнения асимптот;
г) координаты центра симметрии графика функции.

Задание № 13.20. Не выполняя построения графика функции у = (х – 1)^–2 – 2, укажите:
а) область определения и область значений функции;
б) промежутки монотонности и промежутки знакопостоянства функции;
в) уравнения асимптот;
г) уравнение оси симметрии графика функции.

Задание № 13.21.

Задание № 13.22.

Задание № 13.23.

Задание № 13.24.

Задание № 13.25.

 

---

Вы смотрели: ГДЗ Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович. ГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИ. § 13. Функции у = х^–n (n ∈ N), их свойства и графики. ОТВЕТЫ на задачи 13.1 — 13.25.

ОГЛАВЛЕНИЕ Вернуться к списку тем учебника