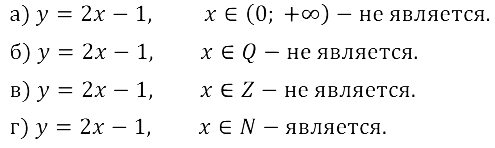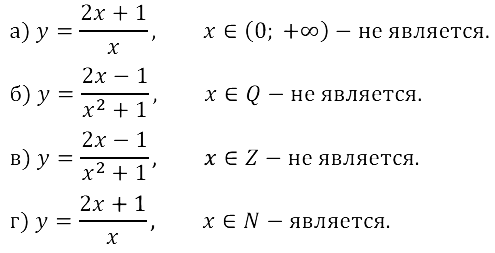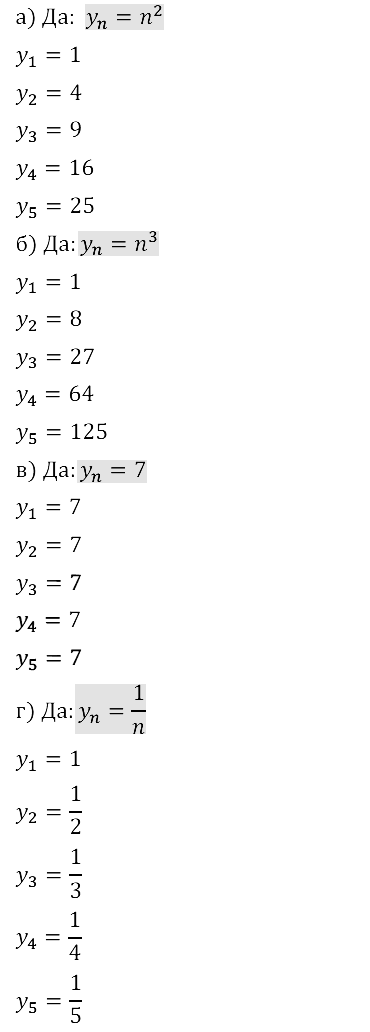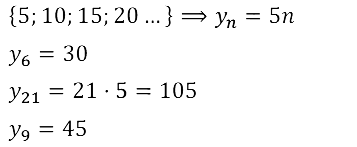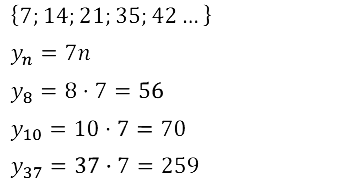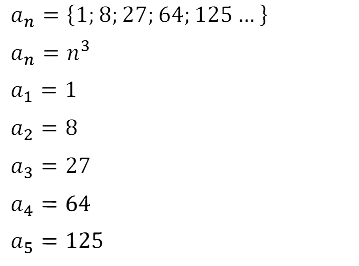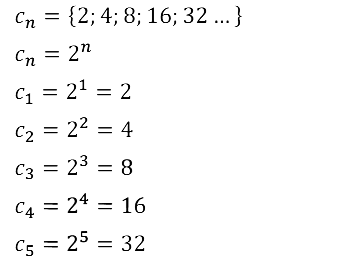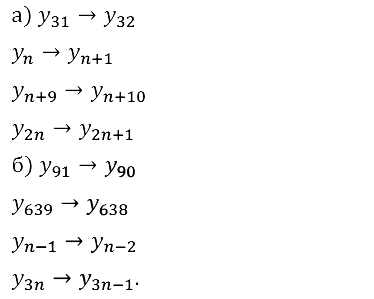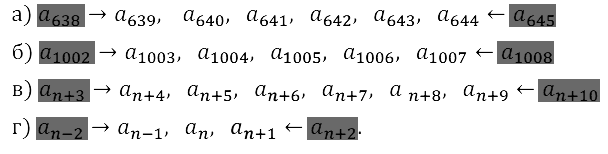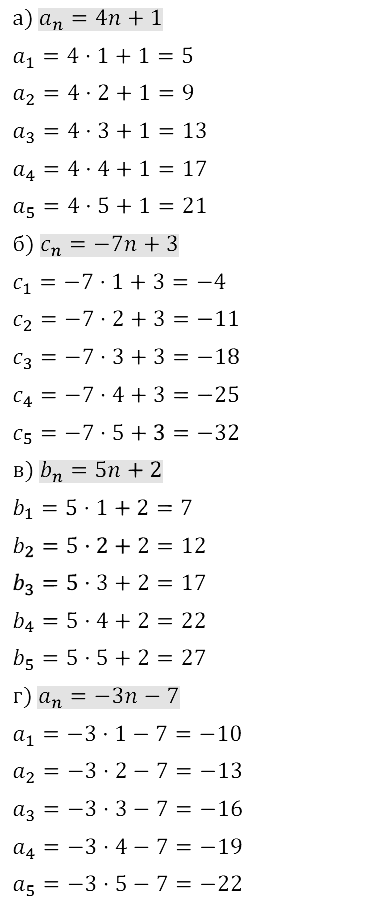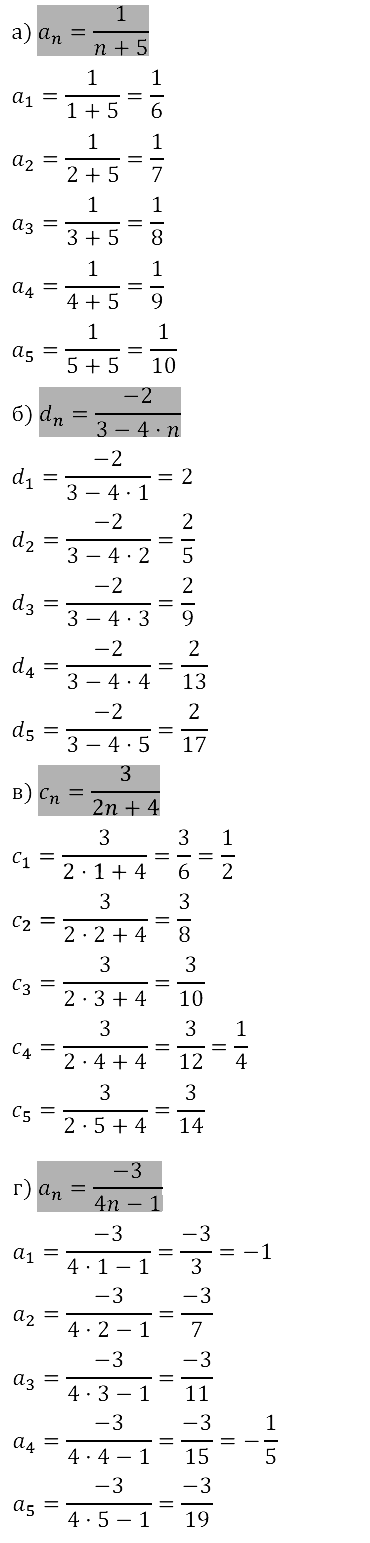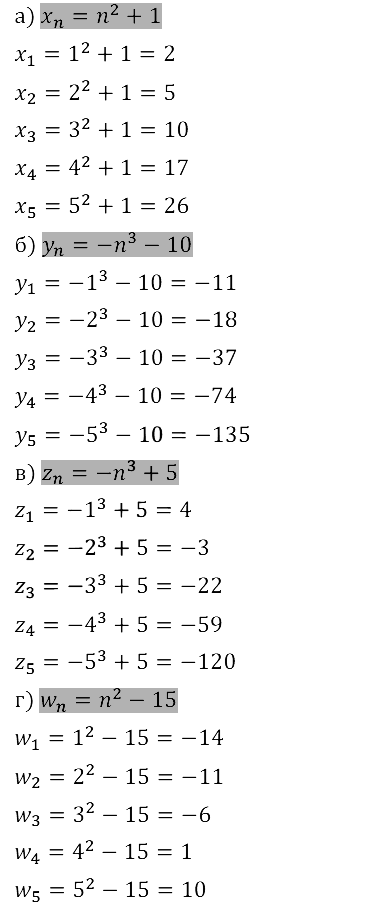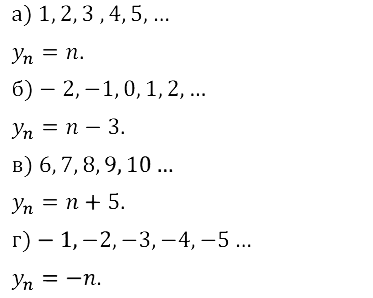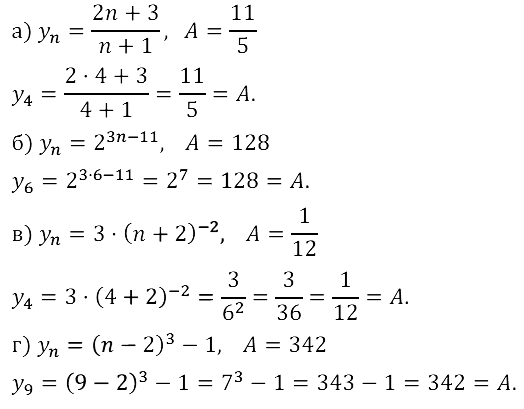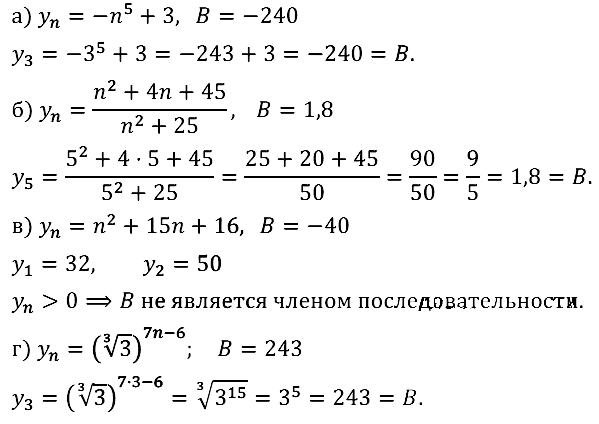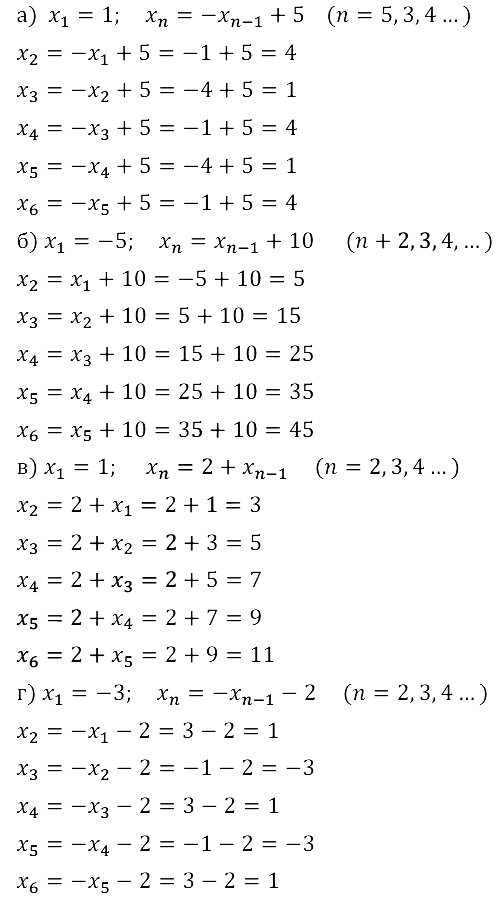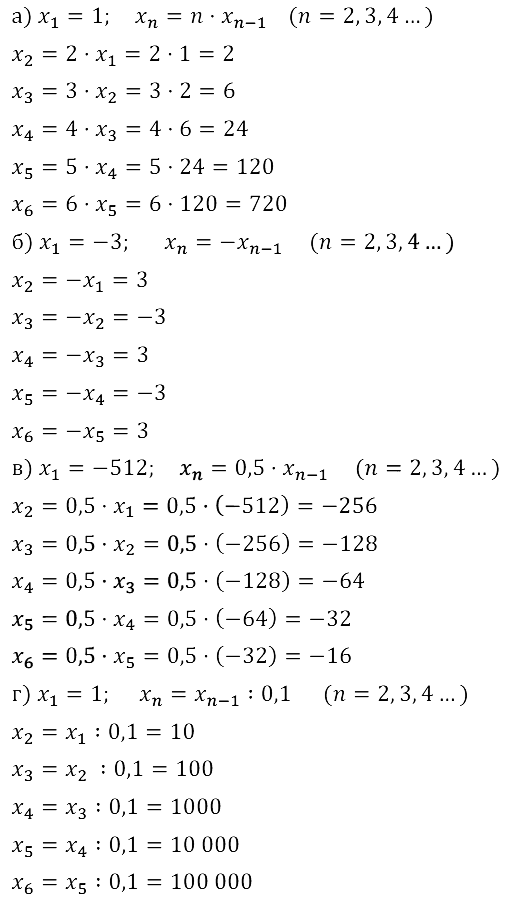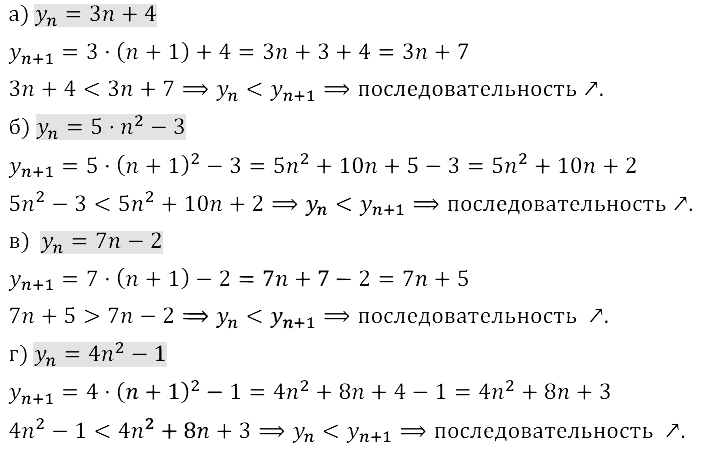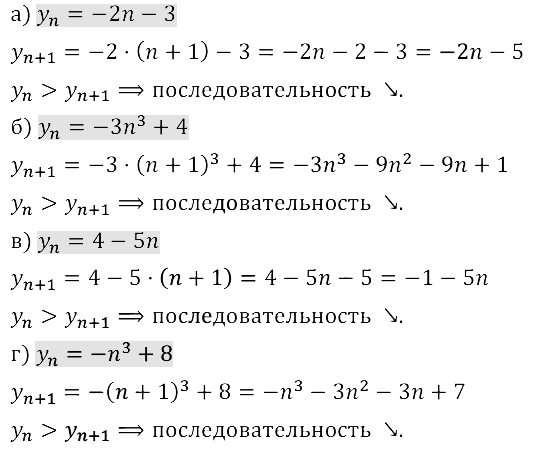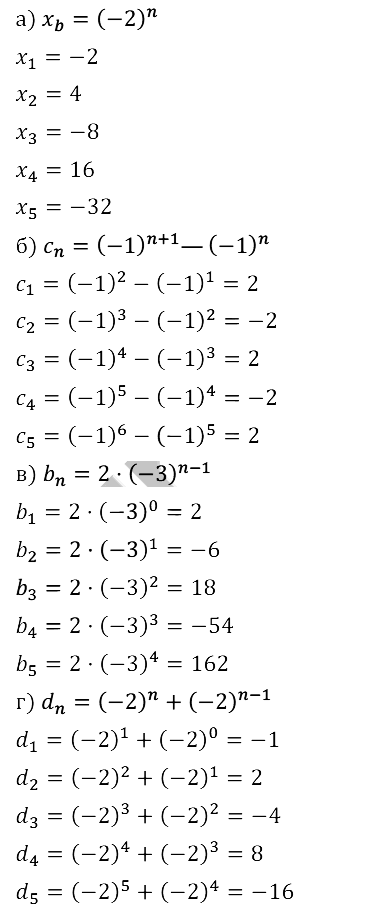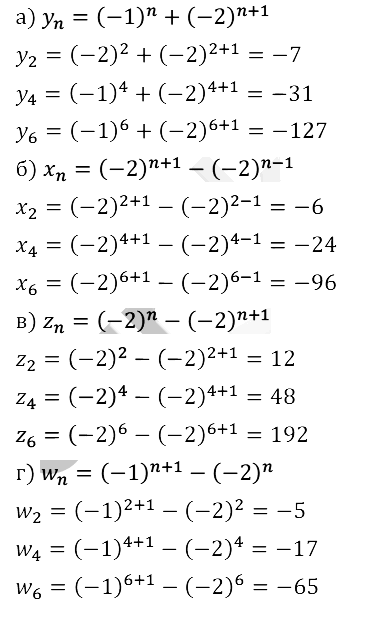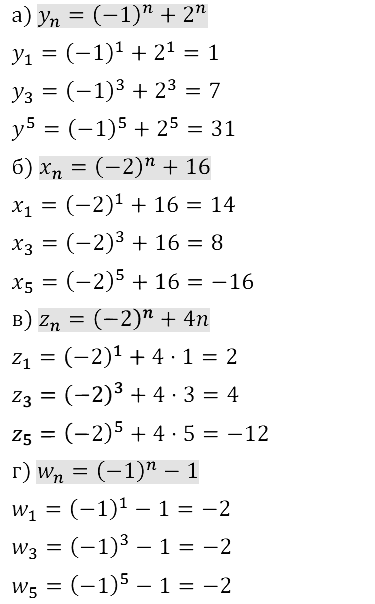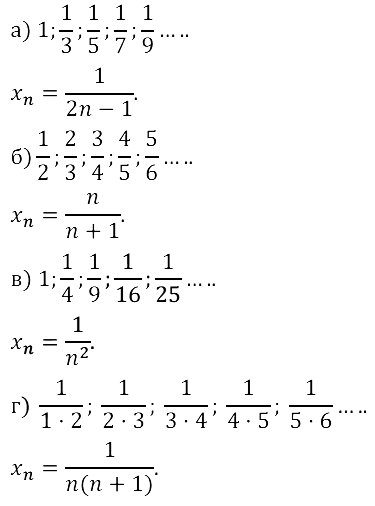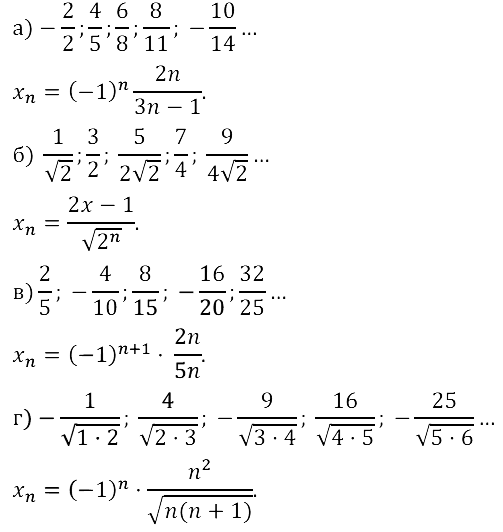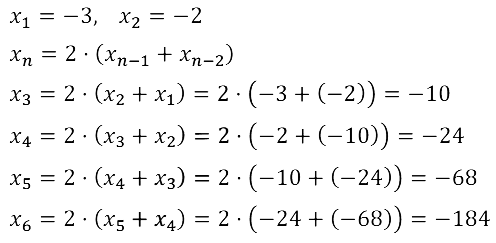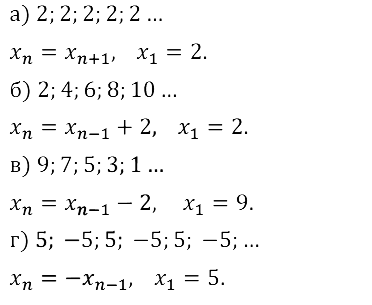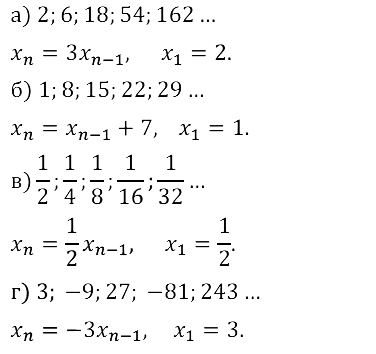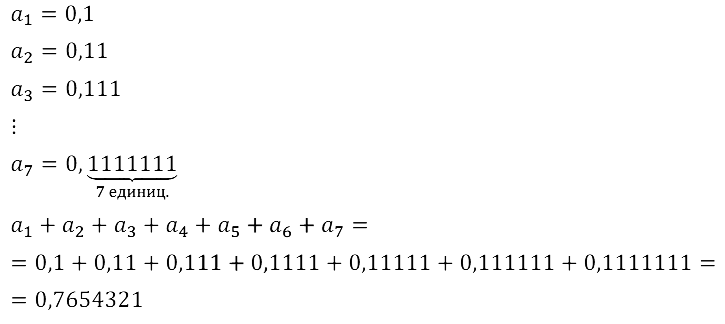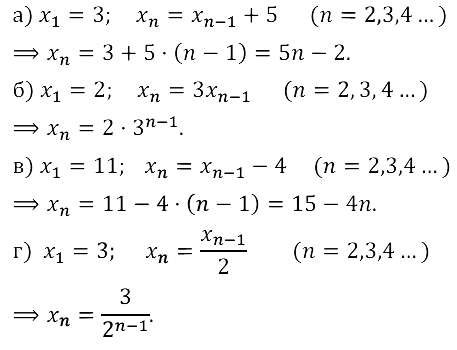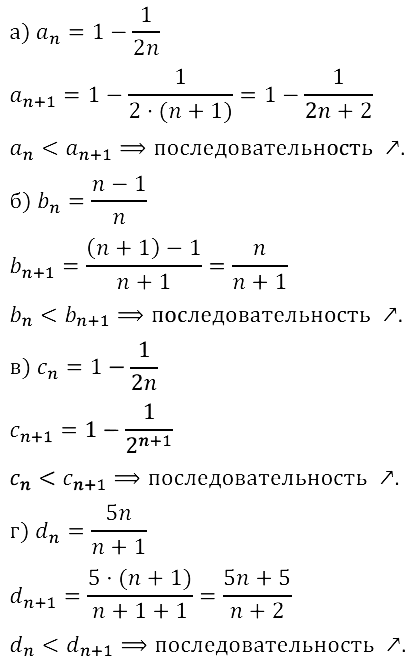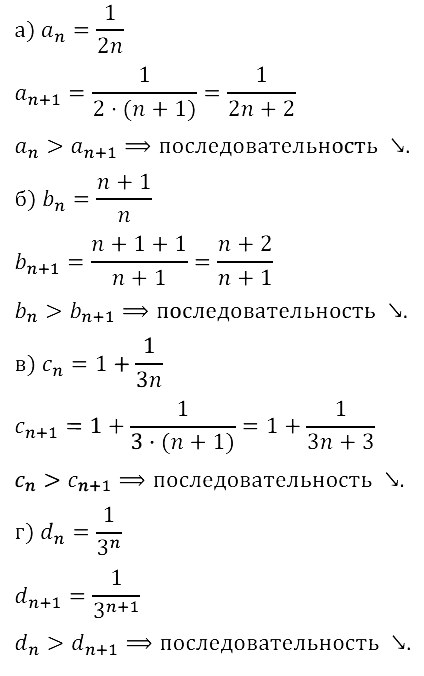Частная школа. 9 класс

Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2020-2023). ОТВЕТЫ на упражнения 15.1 — 15.42. § 15. Числовые последовательности. ГЛАВА 4. ПРОГРЕССИИ.

ОГЛАВЛЕНИЕ Вернуться к списку тем учебника

 

Алгебра 9 класс (Мордкович)
Упражнения №№ 15.1 — 15.42

Нажмите на спойлер, чтобы посмотреть ответ на задание.

ГЛАВА 4. ПРОГРЕССИИ

§ 15. Числовые последовательности

Задание № 15.1. а) у = 2х – 1, x ∈ (0; +∞); б) у – 2х – 1, х ∈ Q; в) у = 2х – 1, х ∈ Z; г) у = 2х – 1, х ∈ N.

Задание № 15.2. a) y = (2х + 1)/x, x ∈ (0; +∞); б) …

Задание № 15.3. Составьте математическую модель следующей задачи. Сосулька тает со скоростью 5 капель в мин. Сколько капель упадёт на землю через 1 мин, 2 мин, 3 мин, 17 мин и т. д. от начала таяния сосульки? Является ли эта математическая модель числовой последовательностью?

Задание № 15.4. Выясните, является ли указанное ниже соответствие последовательностью. Если да, то составьте формулу n–го члена последовательности и найдите её первые пять членов:
а) каждому натуральному числу ставится в соответствие его квадрат;
б) каждому натуральному числу ставится в соответствие его куб;
в) каждому натуральному числу ставится в соответствие число 7;
г) каждому натуральному числу ставится в соответствие обратное число.

Задание № 15.5. Назовите член последовательности (у_n), который:
а) следует за членом у₃₁, у_n, у_n+9, y_2n;
б) предшествует члену у₉₁, у₆₃₉, y_n–1, у_3n.

Задание № 15.6. Назовите все члены последовательности (а_n), которые расположены между членами:
а) а₆₃₈ и а₆₄₅; б) а₁₀₀₂ и а₁₀₀₈; в) а_n+3 и а_n+10; г) а_n–2 и а_n+2.

Задание № 15.7. Найдите несколько начальных членов возрастающей последовательности всех натуральных чисел, кратных пяти. Укажите её шестой, девятый, двадцать первый, n–й члены.

Задание № 15.8. Найдите несколько начальных членов возрастающей последовательности всех натуральных чисел, кратных семи. Укажите её восьмой, десятый, тридцать седьмой, n–й члены.

Задание № 15.9. Известно, что (а_n) — возрастающая последовательность кубов всех натуральных чисел. Найдите а₁, а₂, а₃, а₄, а_n.

Задание № 15.10. Известно, что (с_n) — возрастающая последовательность всех натуральных степеней числа 2. Найдите с₁, с₂, с₃, с₄, с_n.

Задание № 15.11. Известно, что (х_n) — возрастающая последовательность всех натуральных чисел, которые при делении на 3 дают в остатке 2. Найдите x₁, х₈, х₄₅.

Задание № 15.12.

Задание № 15.13.

Задание № 15.14.

Задание № 15.15.

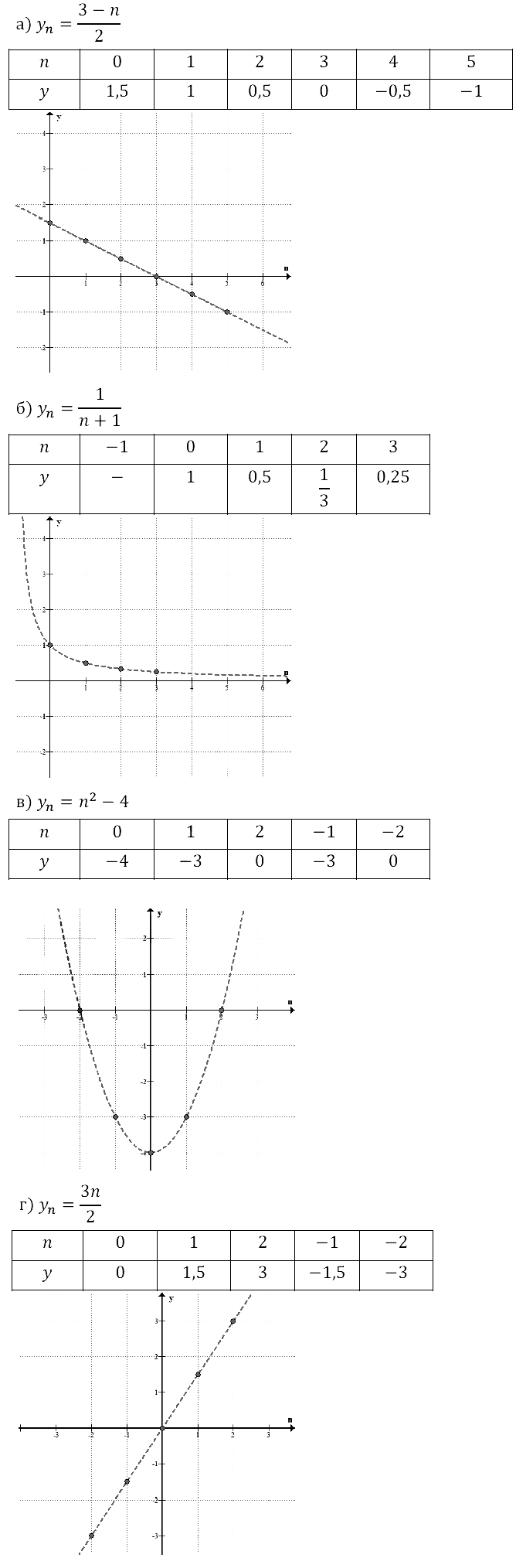
Задание № 15.16.

Задание № 15.17.

Задание № 15.18.

Задание № 15.19.

Задание № 15.20.

Задание № 15.21.

Задание № 15.22.

Задание № 15.23.

Задание № 15.24.

Задание № 15.25.

Задание № 15.26.

Задание № 15.27.

Задание № 15.28.

Задание № 15.29.

Задание № 15.30.

Задание № 15.31.

Задание № 15.32.

Задание № 15.33.

Задание № 15.34.

Задание № 15.35.

Задание № 15.36.

Задание № 15.37.

Задание № 15.38.

Задание № 15.39.

Задание № 15.40.

Задание № 15.41.

Задание № 15.42.

 

---

Вы смотрели: ГДЗ Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович. ГЛАВА 4. ПРОГРЕССИИ. § 15. Числовые последовательности. ОТВЕТЫ на задачи 15.1 — 15.42.

ОГЛАВЛЕНИЕ Вернуться к списку тем учебника