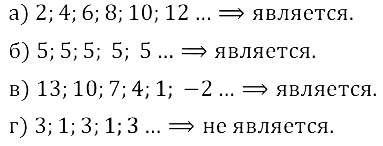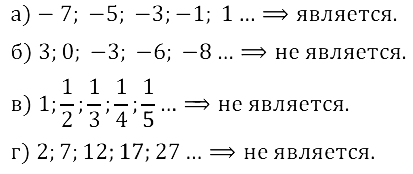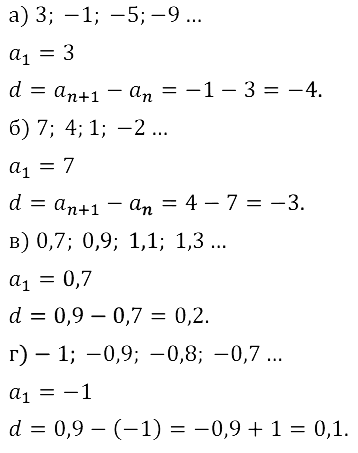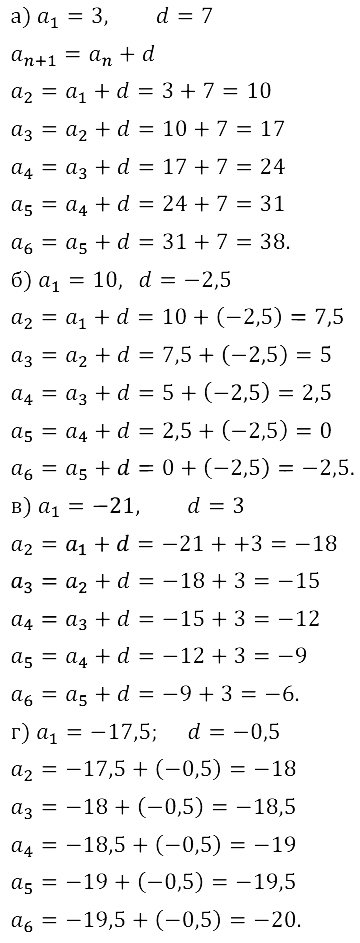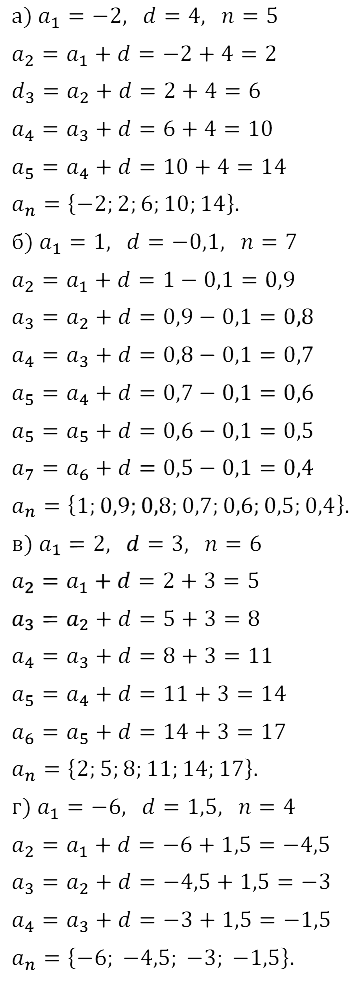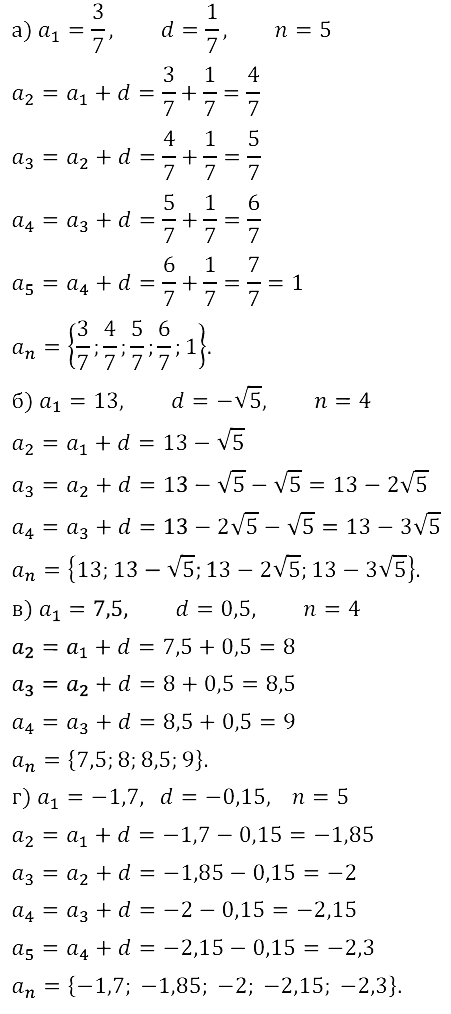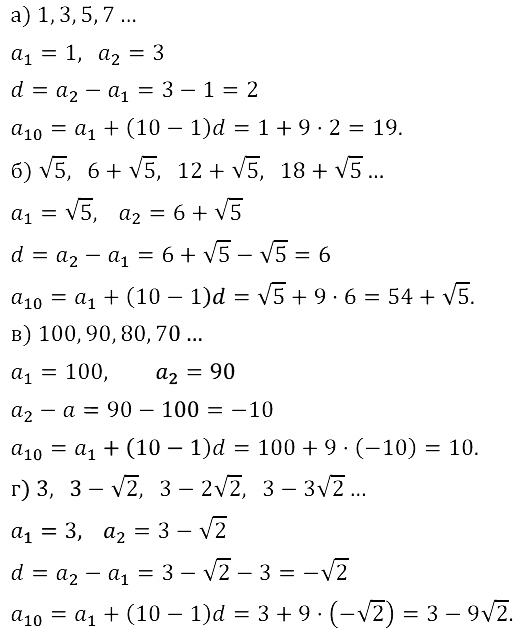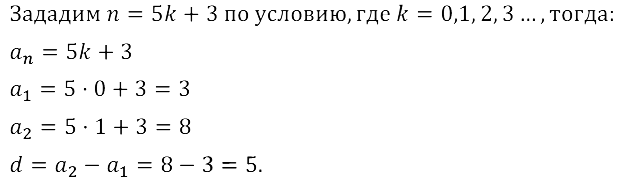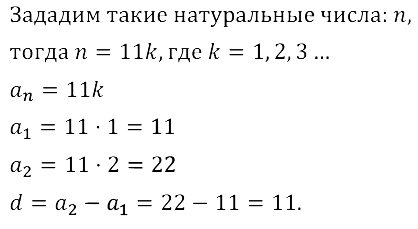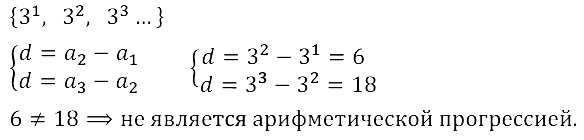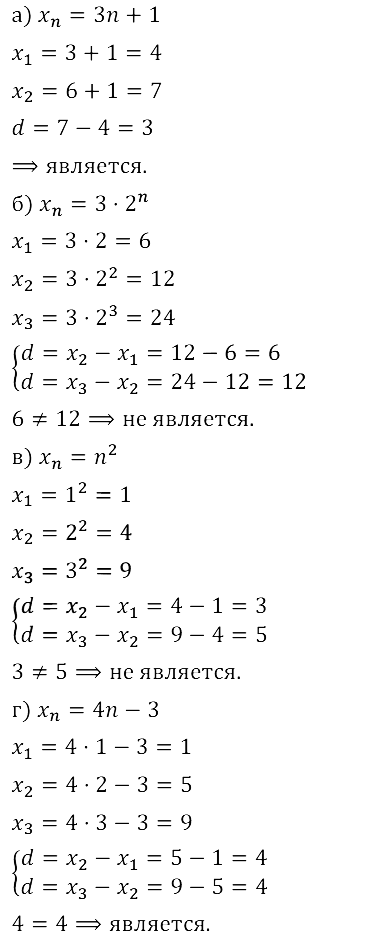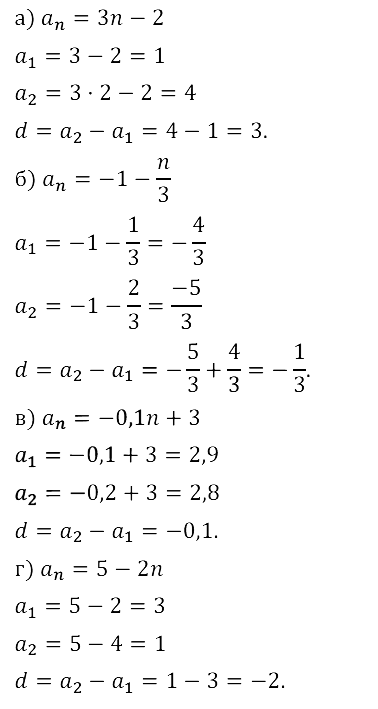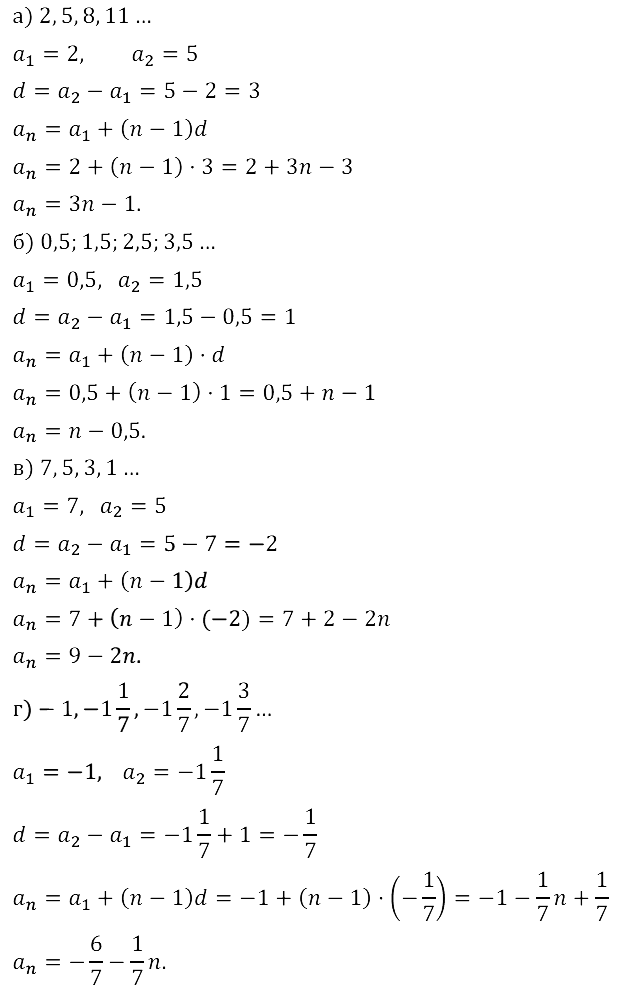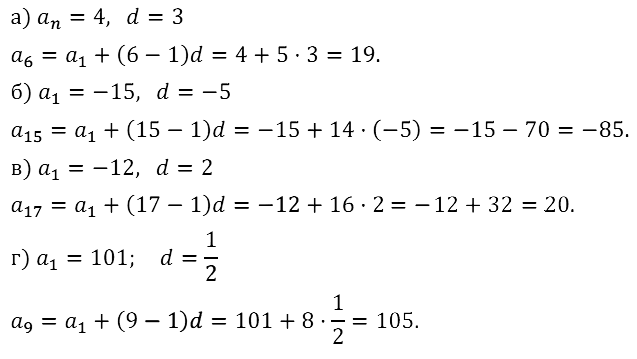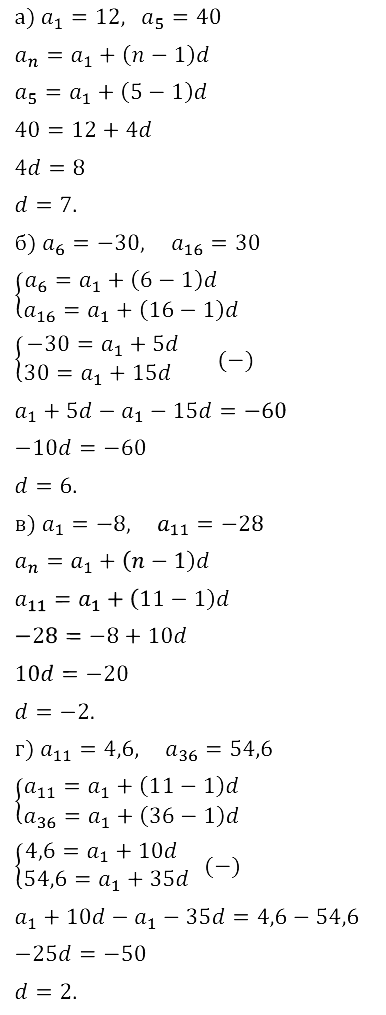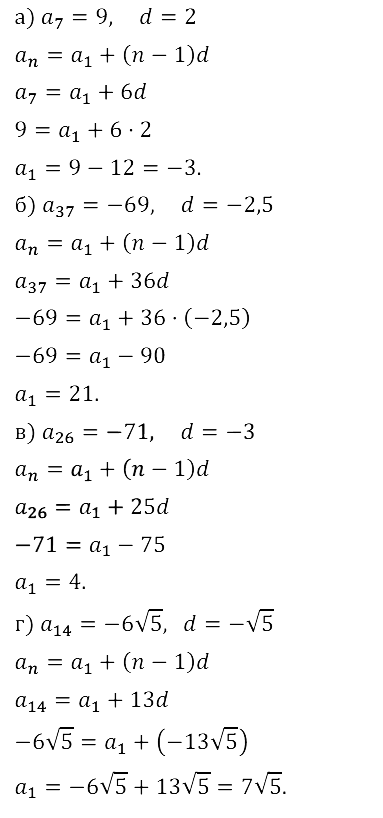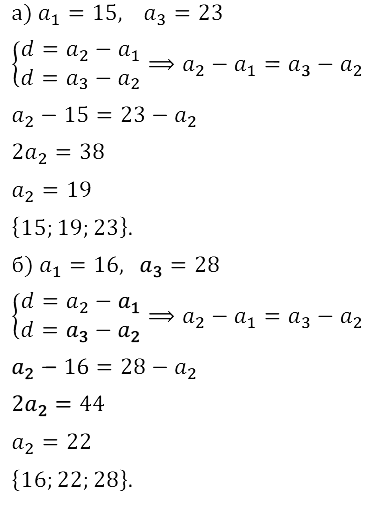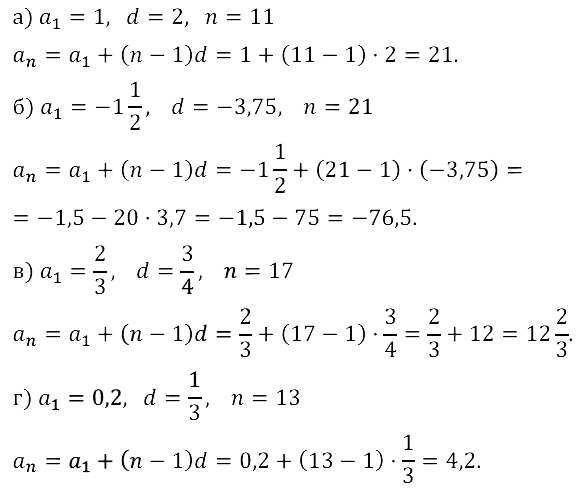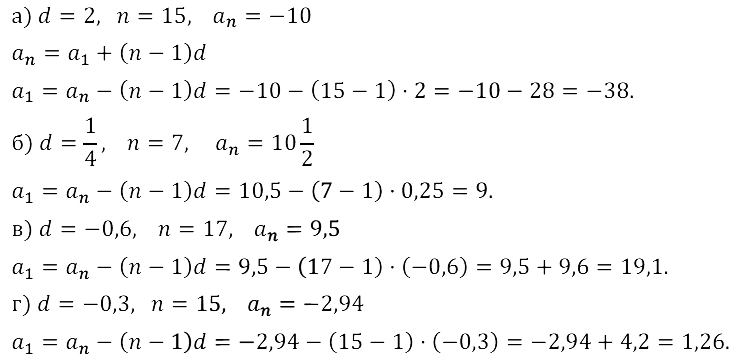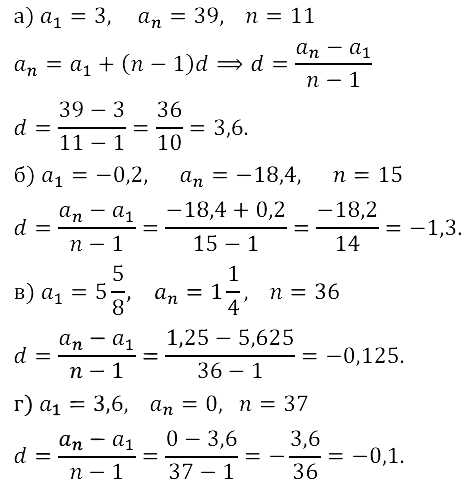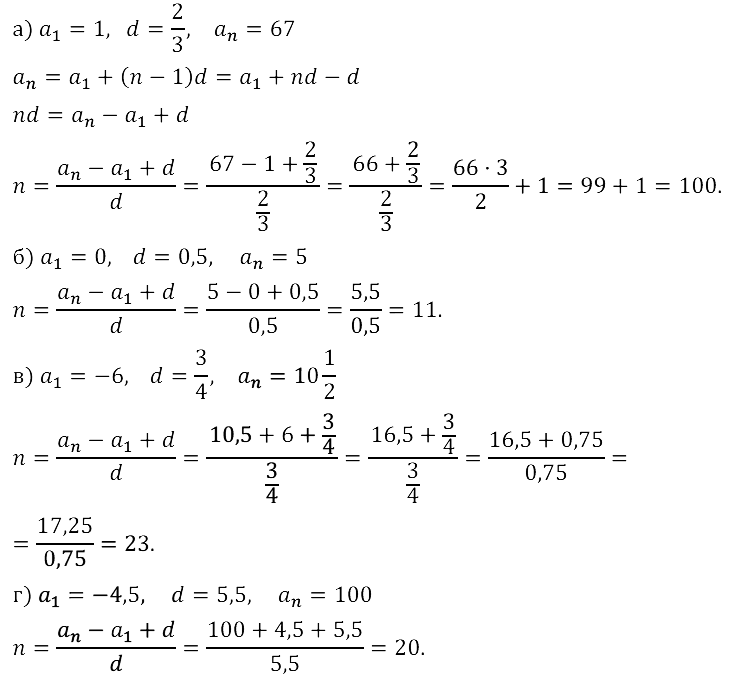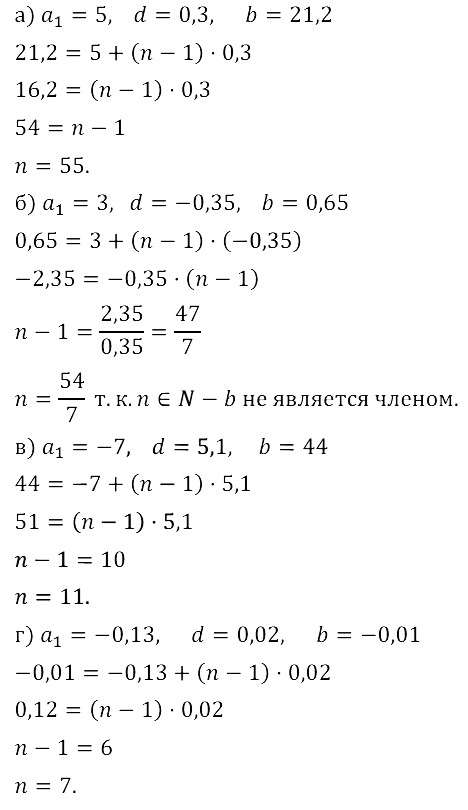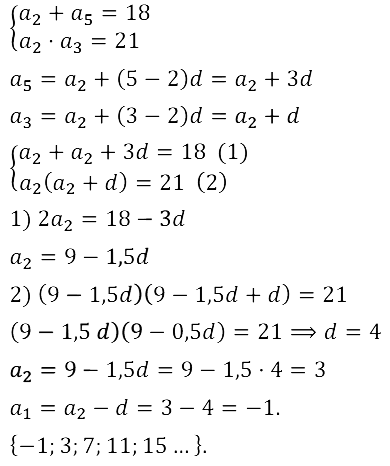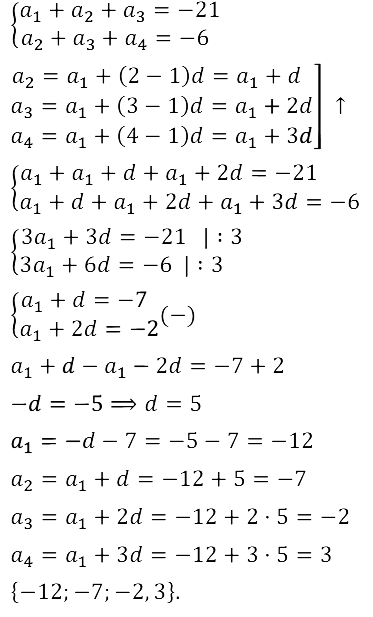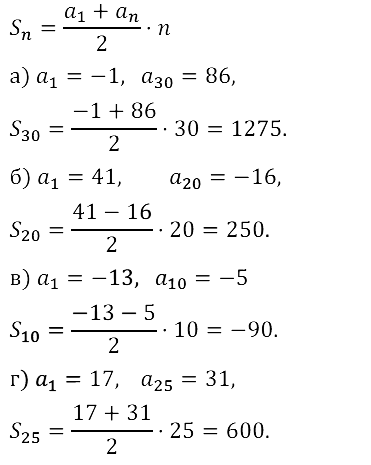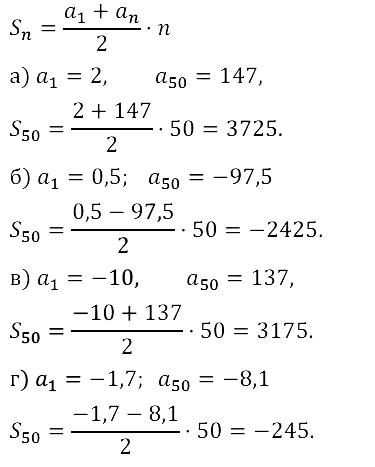Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2020-2023). ОТВЕТЫ на упражнения 16.1 — 16.34. § 16. Арифметическая прогрессия. ГЛАВА 4. ПРОГРЕССИИ.
ОГЛАВЛЕНИЕ Вернуться к списку тем учебника
Алгебра 9 класс (Мордкович)
Упражнения №№ 16.1 — 16.34
Нажмите на спойлер, чтобы посмотреть ответ на задание.
ГЛАВА 4. ПРОГРЕССИИ
§ 16. Арифметическая прогрессия
Определите, является ли приведённая ниже последовательность арифметической прогрессией:
Задание № 16.1. а) 2, 4, 6, 8, 10, 12, …; б) 5, 5, 5, 5, 5, 5, …; в) 13, 10, 7, 4, 1, –2, …; г) 3, 1, 3, 1, 3, 1, ….
Задание № 16.2. а) –7, –5, –3, –1, 1, …; б) 3, 0, –3, –6, –8, …; в) 1, 1/2, 1/3, 1/4, 1/5, …; г) 2, 7, 12, 17, 27, … .
Задание № 16.3. Найдите первый член и разность арифметической прогрессии:
а) 3, –1, –5, –9, …; б) 7, 4, 1, –2, …; в) 0,7, 0,9, 1,1, 1,3, …; г) –1, –0,9, –0,8, –0,7, … .
Задание № 16.4. Выпишите первые шесть членов арифметической прогрессии (аn), если:1
а) a1 = 3, d = 7; б) а1 = 10, d = –2,5; в) а1 = –21, d = 3; г) а1 = –17,5, d = –0,5.
1 Здесь и далее в этом параграфе через d обозначена разность арифметической прогрессии.
Запишите конечную арифметическую прогрессию (аn), заданную следующими условиями:
Задание № 16.5.
Задание № 16.6.
Задание № 16.7.
Задание № 16.8. Возрастающая последовательность состоит из всех натуральных чисел, которые при делении на 5 дают в остатке 3. Выясните, является ли она арифметической прогрессией. Если да, то укажите первый член и разность прогрессии.
Задание № 16.9. Возрастающая последовательность состоит из всех натуральных чисел, кратных 11. Докажите, что она является арифметической прогрессией; укажите первый член и разность прогрессии.
Задание № 16.10. Возрастающая последовательность состоит из всех натуральных степеней числа 3. Выясните, является ли она арифметической прогрессией. Если да, то укажите первый член и разность прогрессии.
Задание № 16.11. Выясните, является ли арифметической прогрессией последовательность (хn), заданная формулой n–го члена. Если да, то укажите первый член и разность прогрессии.
а) хn = 3n + 1; б) хn = 3 • 2n; в) хn = n2; г) хn = 4п – 3.
Задание № 16.12. Докажите, что последовательность (аn) является арифметической прогрессией, и найдите разность прогрессии: а) аn = 2n + 1; б) аn = 0,5n – 4; в) аn = –Зn + 1; г) an = –1/3 • n – 1.
Задание № 16.13.
Задание № 16.14.
Задание № 16.15.
Задание № 16.16.
Задание № 16.17.
Задание № 16.18.
Задание № 16.19. а) Число 29 является членом арифметической прогрессии 9, 11, 13, …. Найдите номер этого члена,
б) Число 43 является членом арифметической прогрессии 3, 7, 11, … . Найдите номер этого члена.
Задание № 16.20. а) является ли число 4,5 членом арифметической прогрессии –1,5, –1, –0,5, …;
б) является ли число 43,5 членом арифметической прогрессии 7, 5, 11, 14,5, … .
Задание № 16.21. Проверьте:
а) является ли число 41 членом арифметической прогрессии (аn), у которой а1 = –7, d = 4;
б) является ли число –33 членом арифметической прогрессии (аn), у которой а1 = 3, d = –6.
Задание № 16.22. а) Между числами 15 и 23 вставьте число таким образом, чтобы получившиеся три числа являлись последовательными членами арифметической прогрессии.
б) Между числами 16 и 28 вставьте число таким образом, чтобы получившиеся три числа являлись последовательными членами арифметической прогрессии.
Задание № 16.23.
Задание № 16.24.
Задание № 16.25.
Задание № 16.26.
Задание № 16.27.
Задание № 16.28.
Задание № 16.29.
Задание № 16.30.
Задание № 16.31.
Задание № 16.32.
Задание № 16.33.
Задание № 16.34.
Вы смотрели: ГДЗ Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович. ГЛАВА 4. ПРОГРЕССИИ. § 16. Арифметическая прогрессия. ОТВЕТЫ на задачи 16.1 — 16.34.