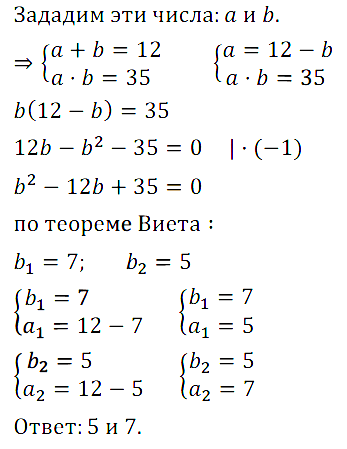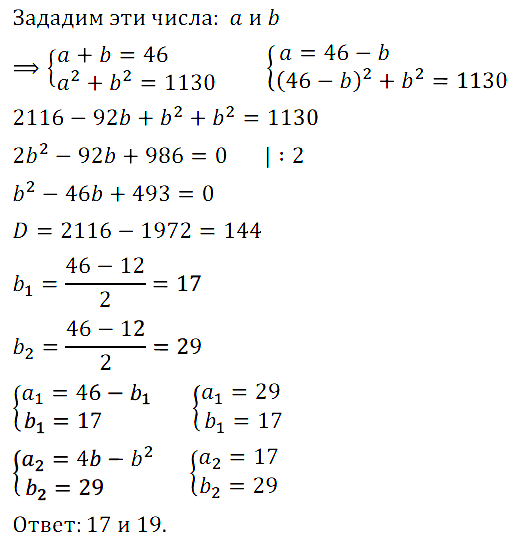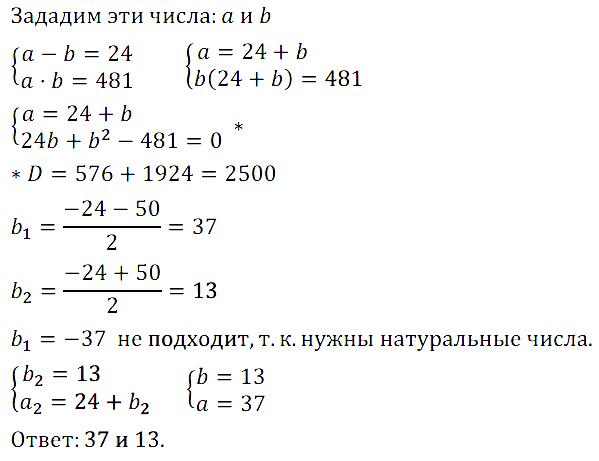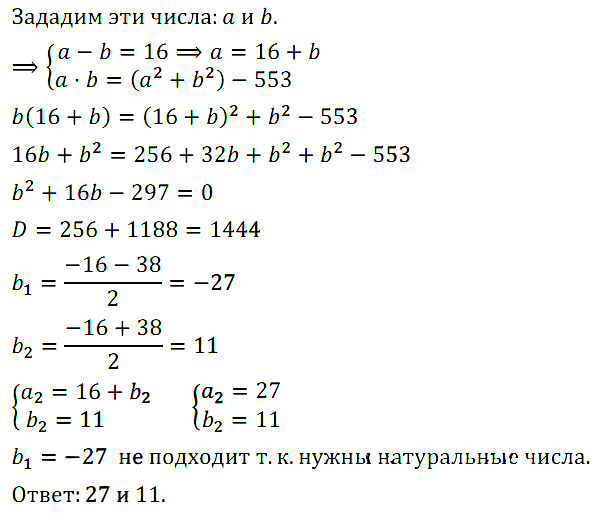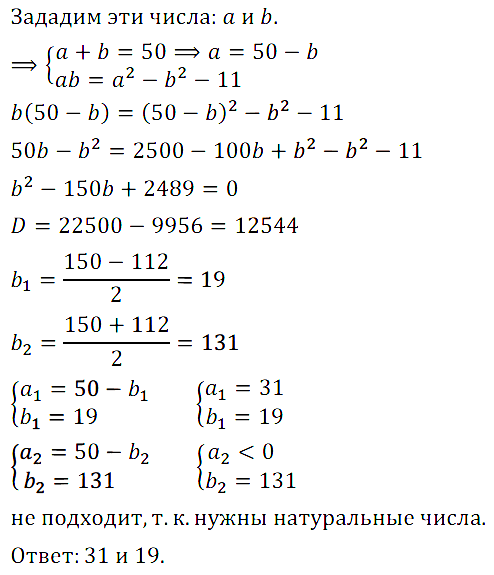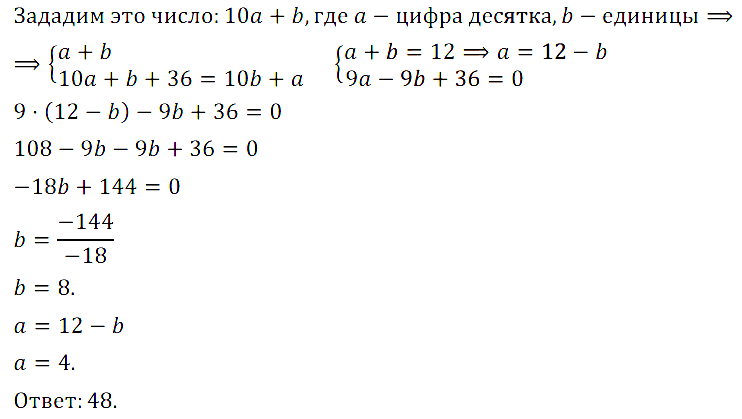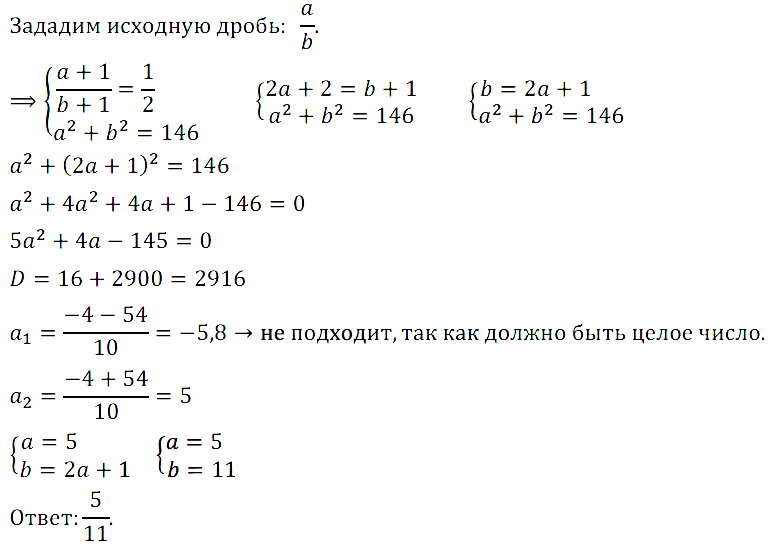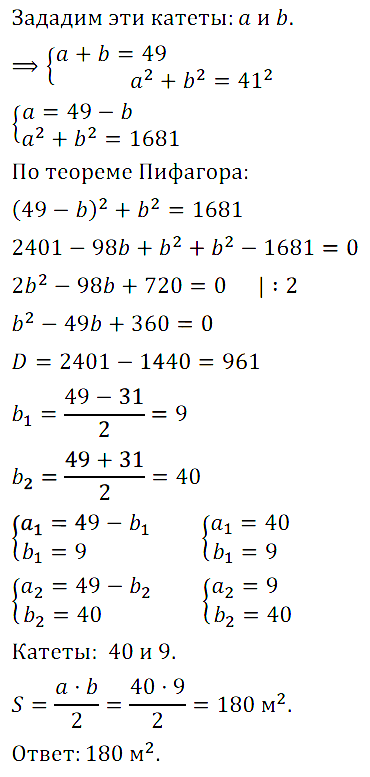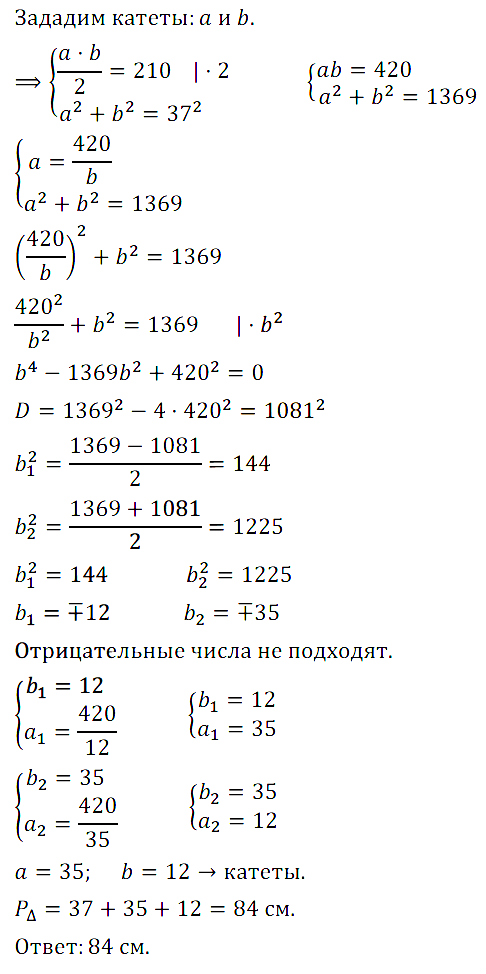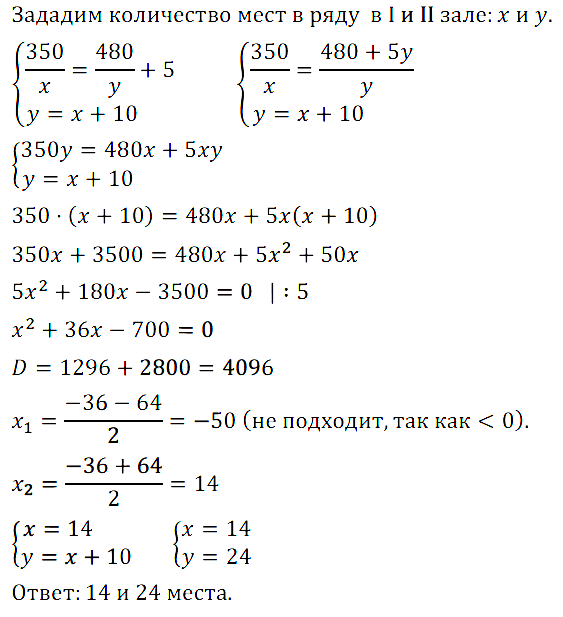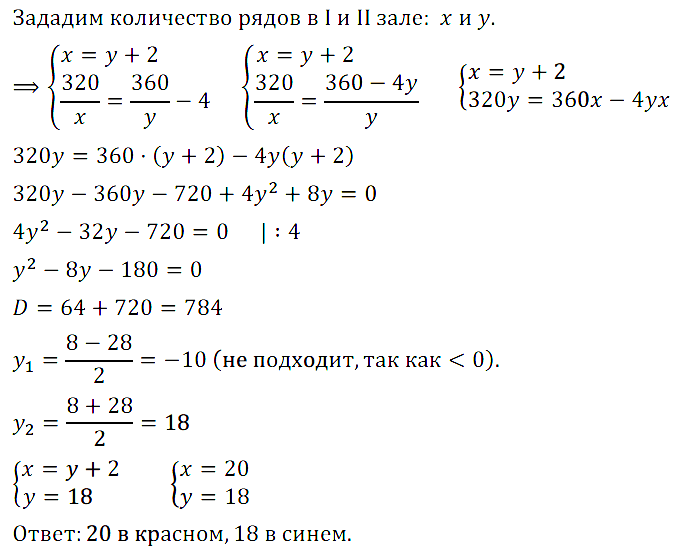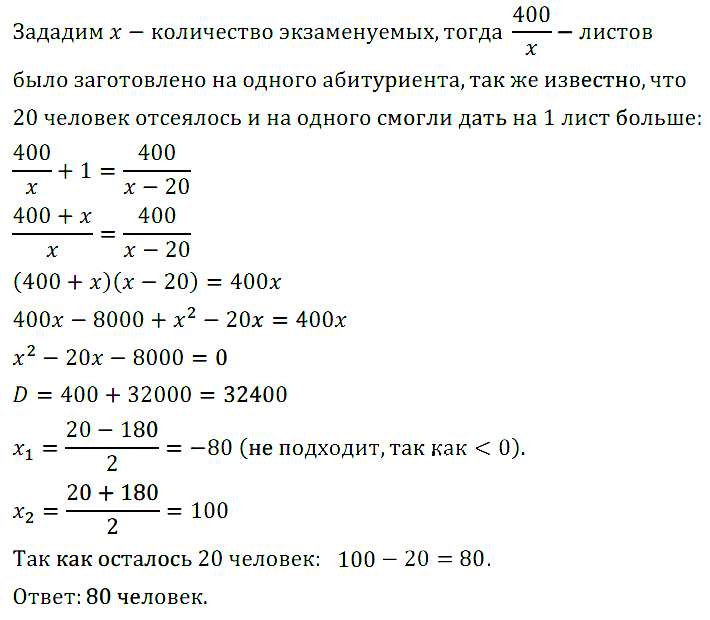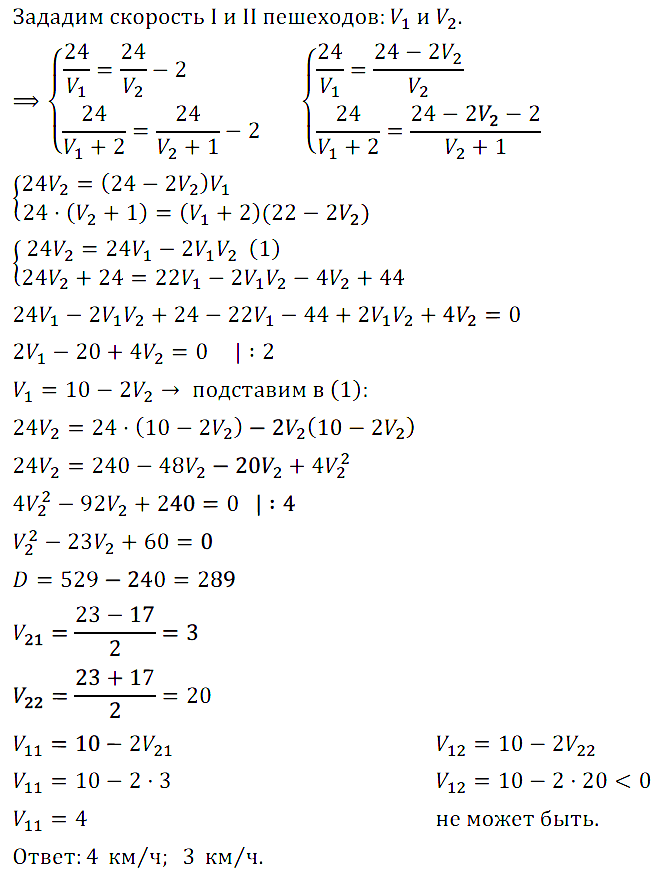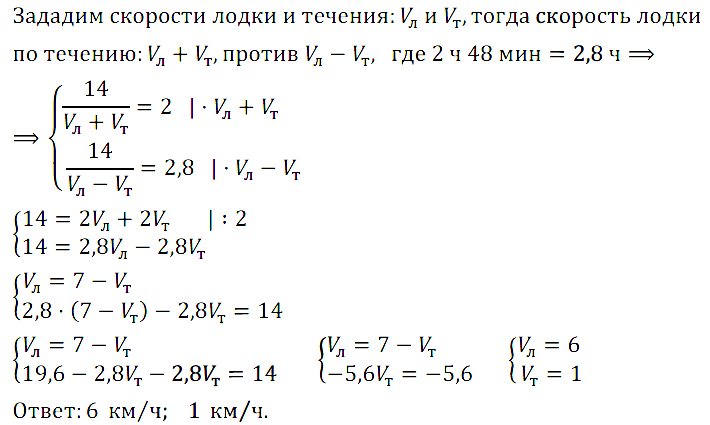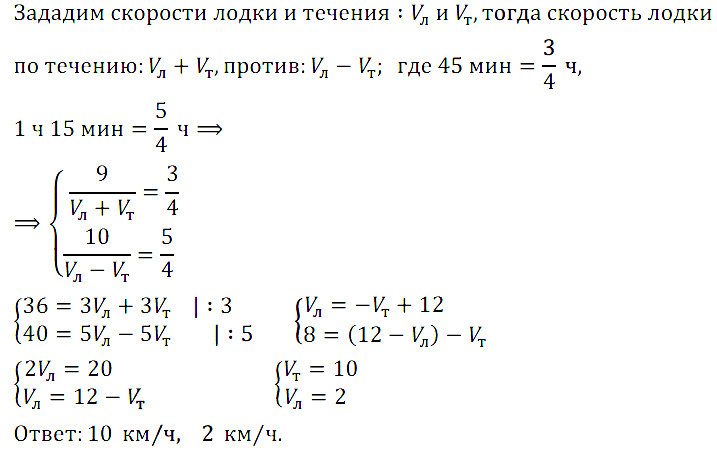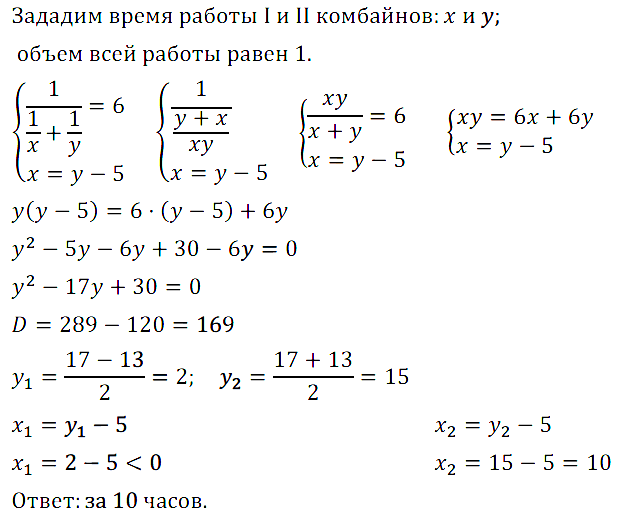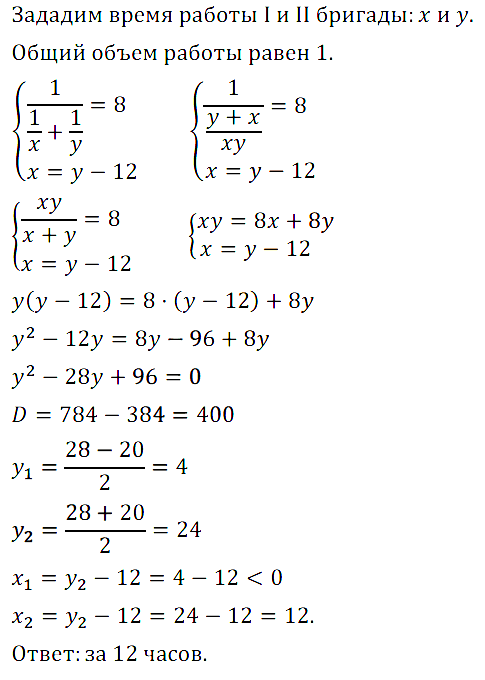Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ОТВЕТЫ на упражнения 7.1 — 7.22. § 7. Системы уравнений как математические модели реальных ситуаций (ГЛАВА 2. СИСТЕМЫ УРАВНЕНИЙ).
ОГЛАВЛЕНИЕ Вернуться к списку тем учебника
Алгебра 9 класс (Мордкович)
Упражнения №№ 7.1 — 7.22
Нажмите на спойлер, чтобы посмотреть ответ на задание.
§ 7. Системы уравнений как математические модели реальных ситуаций
Задание № 7.1. Сумма двух чисел равна 12, а их произведение равно 35. Найдите эти числа.
Задание № 7.2. Сумма двух чисел равна 46, а сумма их квадратов равна 1130. Найдите эти числа.
Задание № 7.3. Разность двух натуральных чисел равна 24, а их произведение равно 481. Найдите эти числа.
Задание № 7.4. Разность двух натуральных чисел равна 16, а произведение на 553 меньше суммы их квадратов. Найдите эти числа.
Задание № 7.5. Сумма двух натуральных чисел равна 50, а произведение на 11 меньше, чем разность их квадратов. Найдите эти числа.
Задание № 7.6. Какое двузначное число в 4 раза больше суммы своих цифр и в 3 раза больше произведения цифр?
Задание № 7.7. Сумма цифр двузначного числа равна 12. Если к заданному числу прибавить 36, то получим число, записанное теми же цифрами, но в обратном порядке. Найдите исходное число.
Задание № 7.8. Если к числителю и знаменателю обыкновенной дроби прибавить по 1, то дробь станет равна 1/2, а если сложить квадраты числителя и знаменателя исходной дроби, то получится 146. Найдите исходную дробь.
Задание № 7.9. Диагональ прямоугольника равна 10 см, а его периметр равен 28 см. Найдите стороны прямоугольника.
Задание № 7.10. Сумма катетов прямоугольного треугольника равна 49 м, а его гипотенуза равна 41 м. Найдите площадь треугольника.
Задание № 7.11. Разность катетов прямоугольного треугольника равна 23 дм, а его гипотенуза равна 37 дм. Найдите периметр треугольника.
Задание № 7.12. Площадь прямоугольного треугольника равна 210 см2, гипотенуза равна 37 см. Найдите периметр этого треугольника.
Задание № 7.13. В первом зрительном зале 350 мест, а во втором — 480. Во втором зале на 5 рядов меньше, чем в первом, но в каждом ряду на 10 мест больше, чем в каждом ряду первого зала. Сколько мест в ряду в каждом зале?
Задание № 7.14. В красном зале кинотеатра 320 мест, а в синем — 360. В красном зале на 2 ряда больше, чем в синем, но в каждом ряду на 4 места меньше, чем в каждом ряду синего зала. Сколько рядов в каждом зале кинотеатра?
Задание № 7.15. В колледже для проведения письменного экзамена по математике было заготовлено 400 листов бумаги. Но на экзаменах по предыдущим предметам отсеялось 20 человек, поэтому каждому абитуриенту смогли дать на 1 лист бумаги больше, чем предполагалось. Сколько человек сдавало экзамен по математике?
Задание № 7.16. Из двух городов, расстояние между которыми 700 км, одновременно навстречу друг другу отправляются два поезда и встречаются через 5 ч. Если второй поезд отправится на 7 ч раньше первого, то они встретятся через 2 ч после отправления первого поезда. Найдите скорость каждого поезда.
Задание № 7.17. Расстояние между двумя посёлками, равное 24 км, первый пешеход преодолел на 2 ч быстрее второго. Если скорость движения первого увеличить на 2 км/ч, а второго на 1 км/ч, то и в этом случае весь путь первый преодолеет на 2 ч быстрее второго. Найдите первоначальные скорости пешеходов.
Задание № 7.18. Расстояние между двумя пунктами по реке равно 14 км. Лодка проходит этот путь по течению за 2 ч, а против течения за 2 ч 48 мин. Найдите собственную скорость лодки и скорость течения реки.
Задание № 7.19. Моторная лодка против течения реки проплыла 10 км, а по течению 9 км, при этом по течению она шла 45 мин, а против течения — 1 ч 15 мин. Найдите собственную скорость лодки и скорость течения реки.
Задание № 7.20. Турист проплыл на лодке по реке из города А в город В и обратно за 7 ч. Найдите скорость течения реки, если известно, что турист проплывал 2 км против течения за то же время, что и 5 км по течению, а расстояние между городами равно 20 км.
Задание № 7.21. Два комбайна, работая совместно, могут выполнить задание за 6 ч. Первый комбайн, работая один, может выполнить это задание на 5 ч скорее, чем второй комбайн. За сколько времени может выполнить задание первый комбайн, работая один?
Задание № 7.22. Две бригады, работая вместе, могут выполнить задание за 8 ч. Первая бригада, работая одна, могла бы выполнить задание на 12 ч быстрее, чем вторая бригада. За сколько часов могла бы выполнить задание первая бригада, если бы она работала одна?
Вы смотрели: ГДЗ Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ГЛАВА 2. СИСТЕМЫ УРАВНЕНИЙ. § 7. Системы уравнений как математические модели реальных ситуаций. ОТВЕТЫ на задачи 7.1 — 7.22.