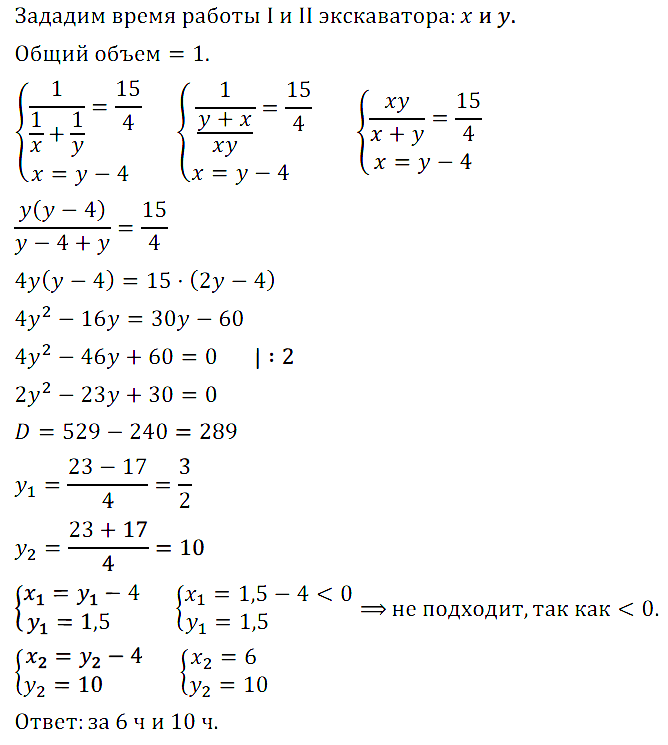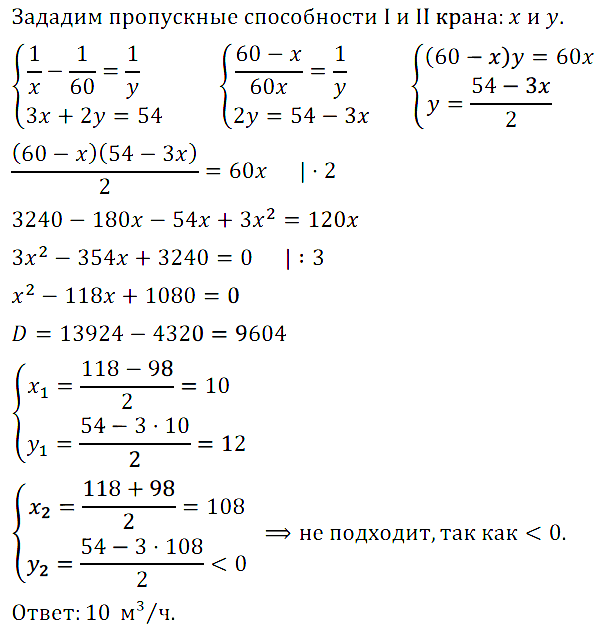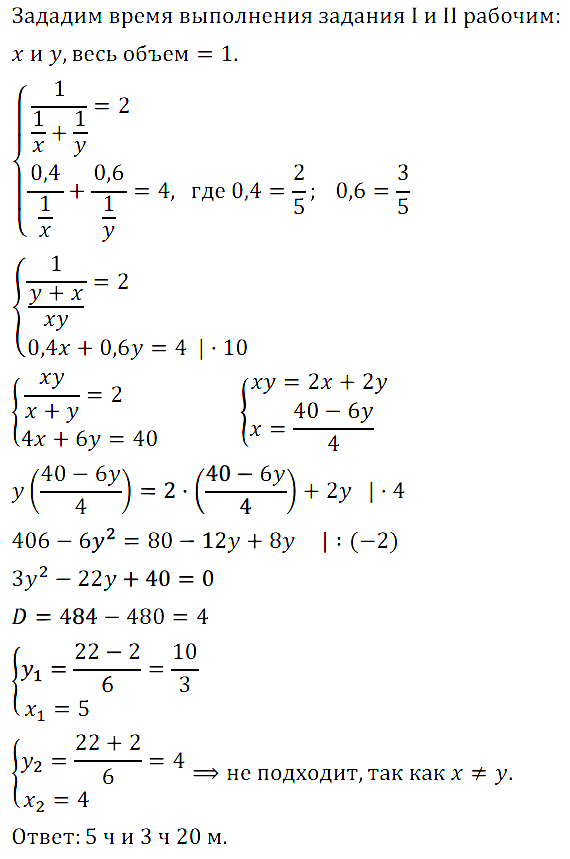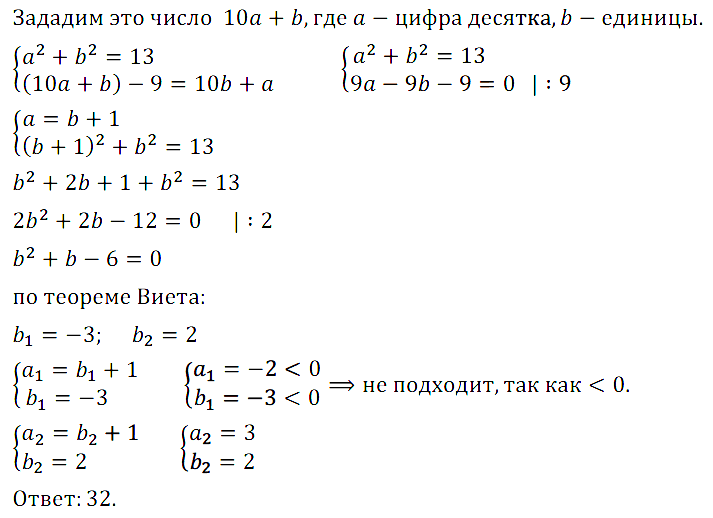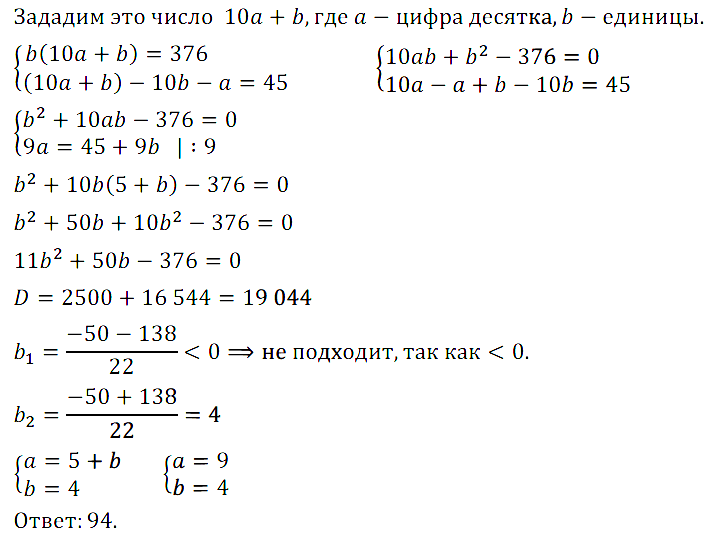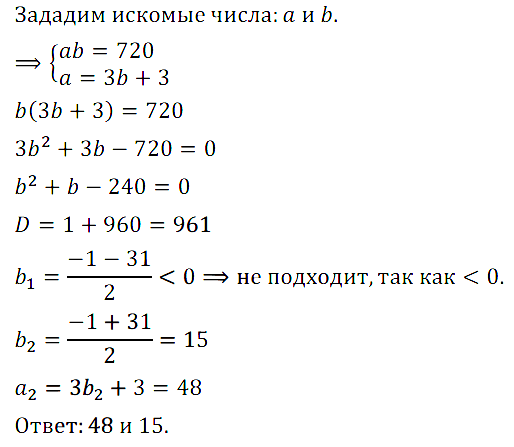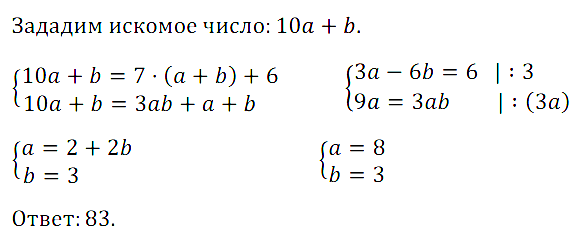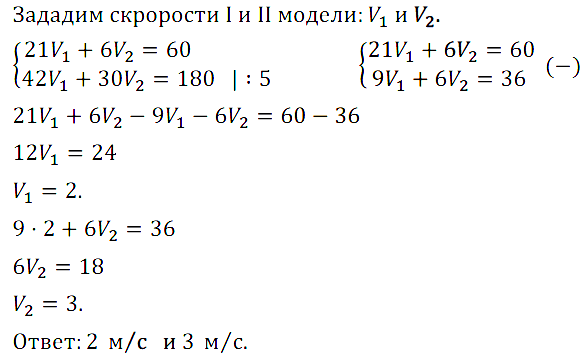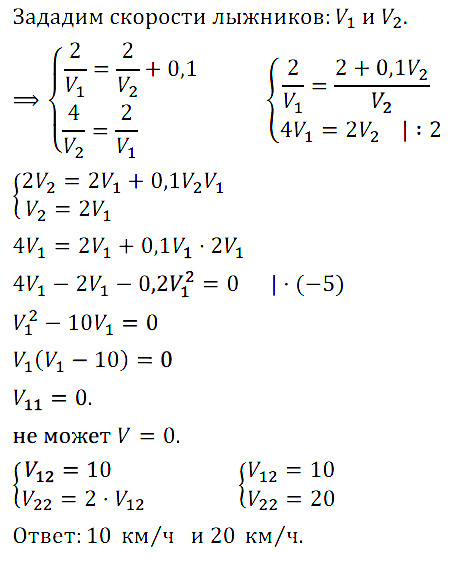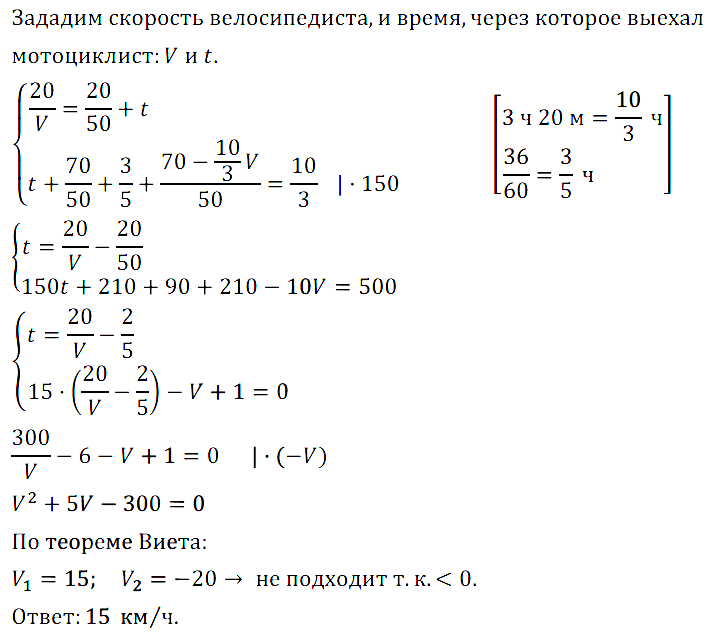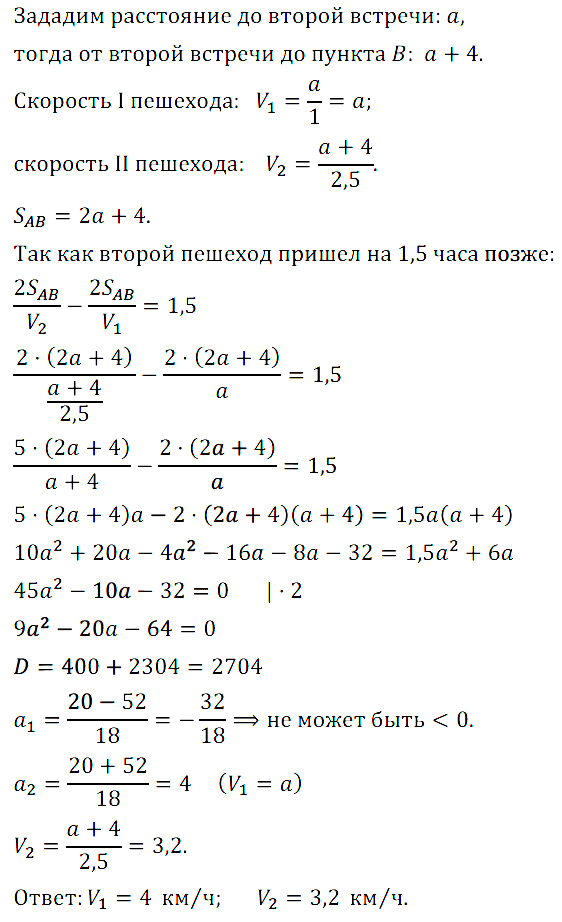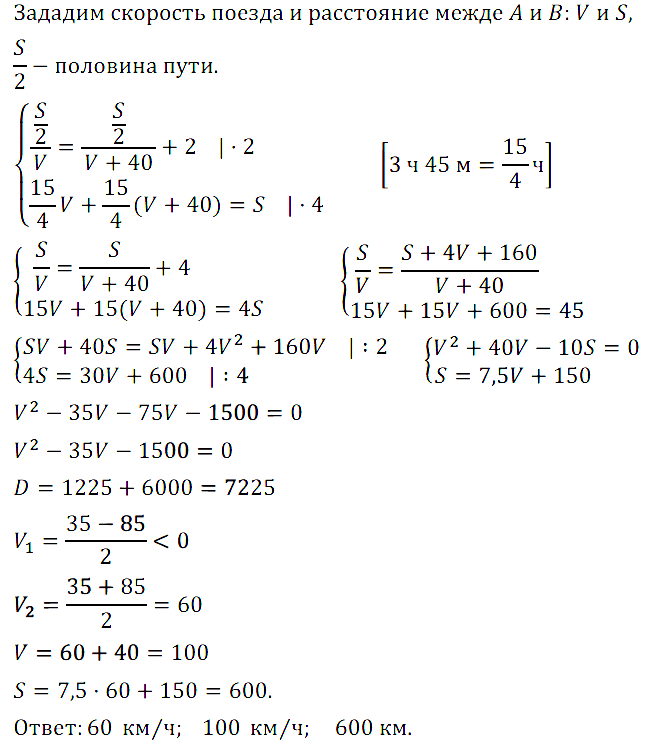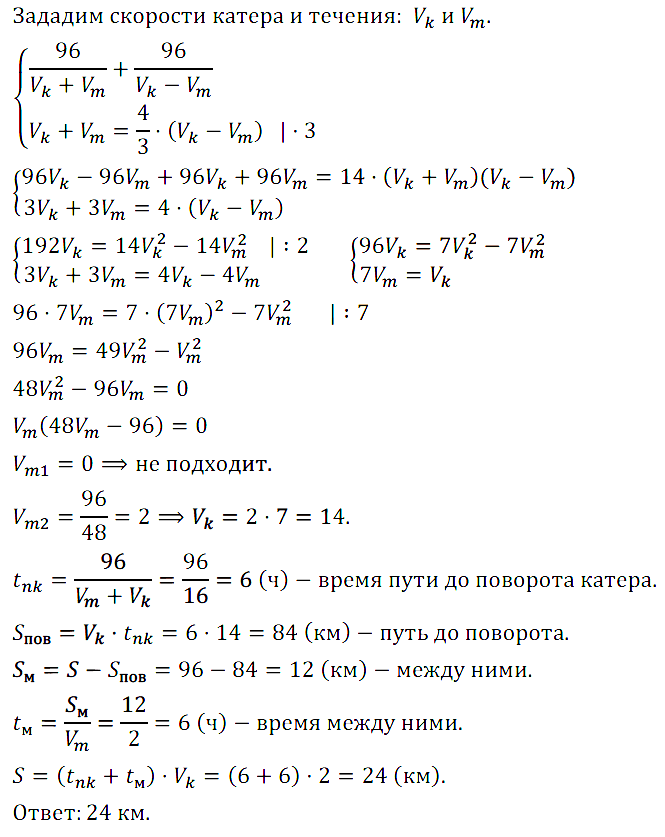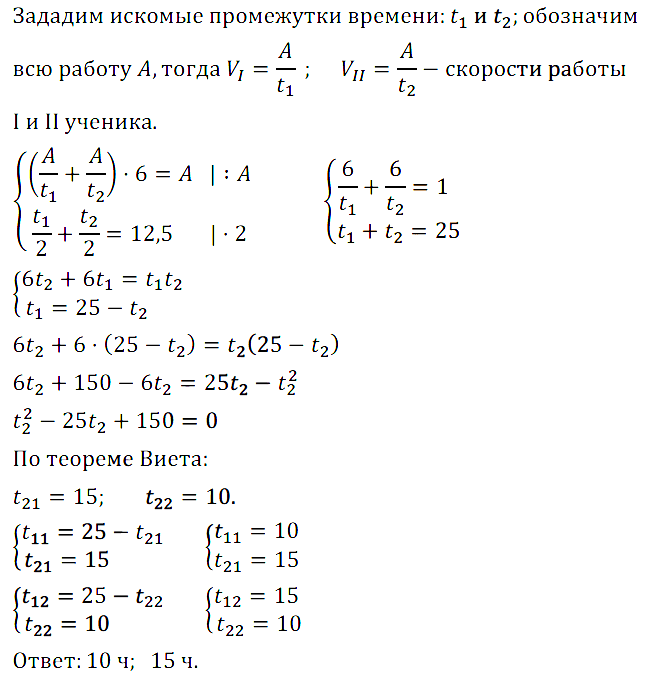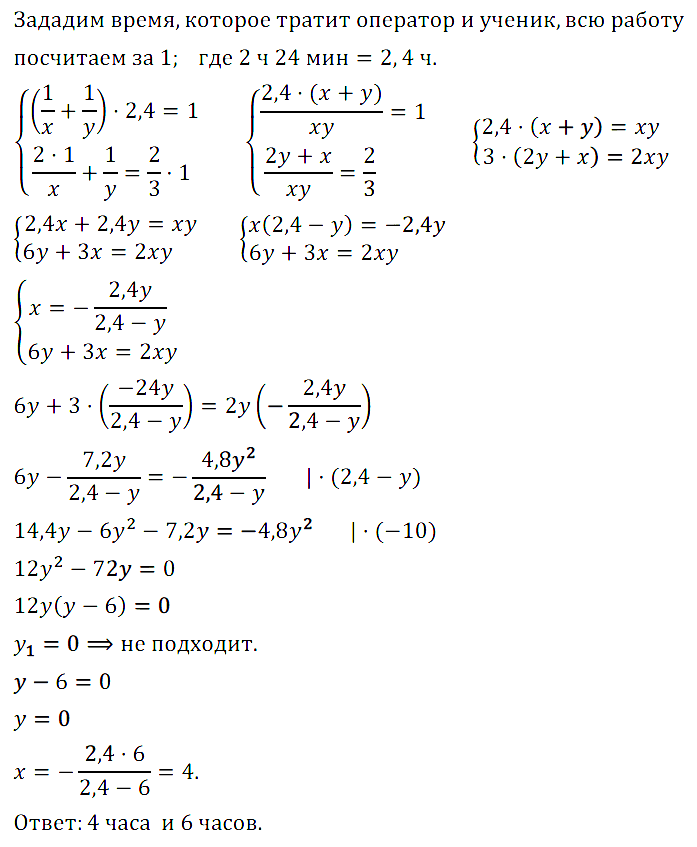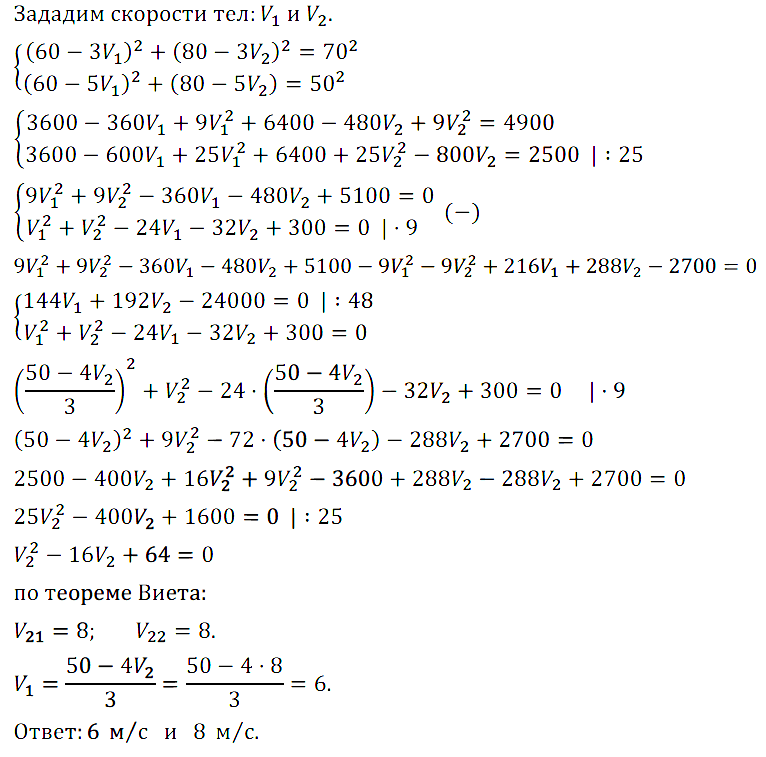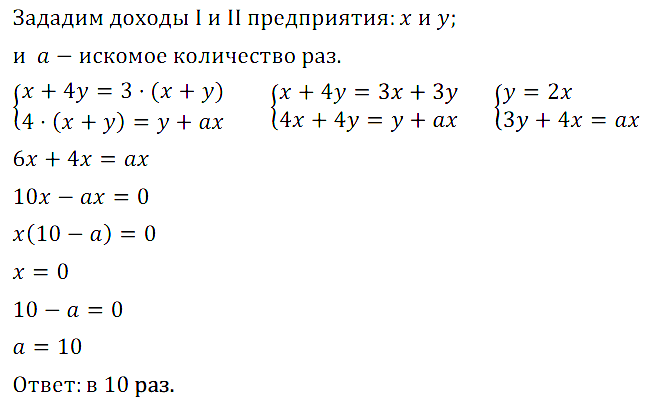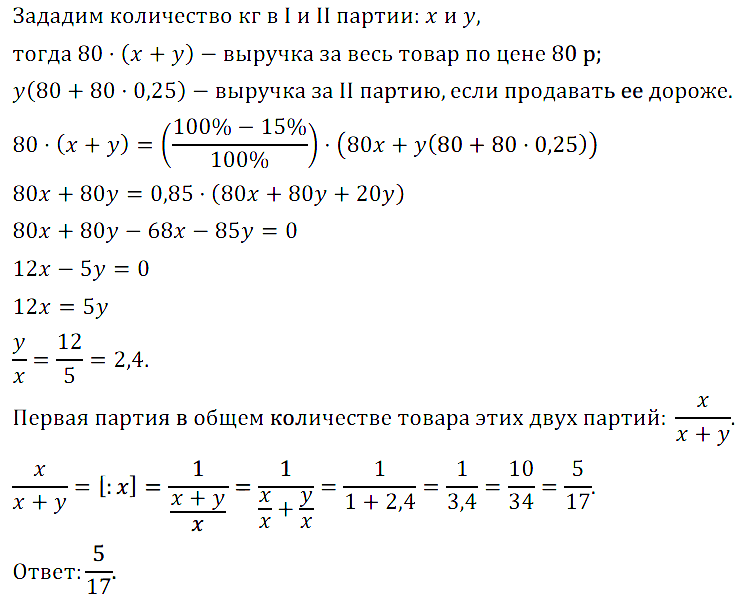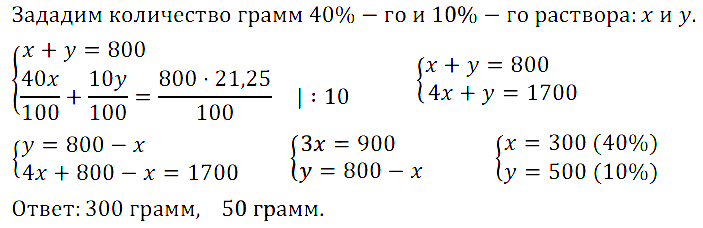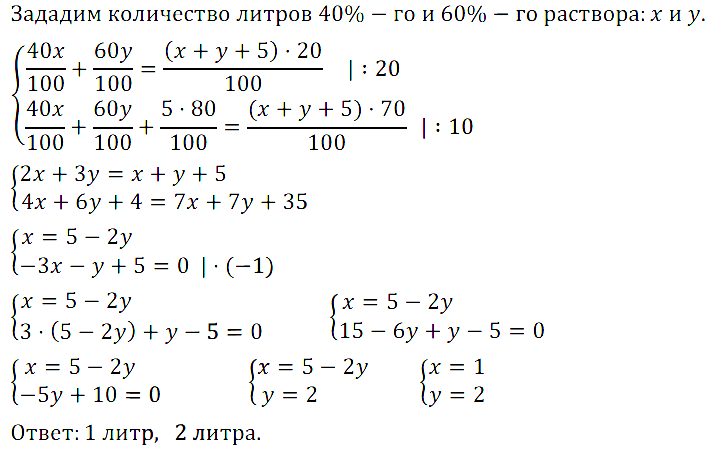Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ОТВЕТЫ на упражнения 7.23 — 7.55. § 7. Системы уравнений как математические модели реальных ситуаций (продолжение). ГЛАВА 2. СИСТЕМЫ УРАВНЕНИЙ.
ОГЛАВЛЕНИЕ Вернуться к списку тем учебника
Алгебра 9 класс (Мордкович)
Упражнения №№ 7.23 — 7.55
Нажмите на спойлер, чтобы посмотреть ответ на задание.
§ 7. Системы уравнений как математические модели реальных ситуаций
Задание № 7.23. Два экскаватора, работая одновременно, выполнят некоторый объём земляных работ за 3 ч 45 мин. Один экскаватор, работая отдельно, может выполнить этот объём работ на 4 ч быстрее, чем другой. Сколько времени требуется каждому экскаватору в отдельности для выполнения того же объёма земляных работ?
Задание № 7.24. Чан наполняется двумя кранами при совместной работе за 1 ч. Наполнение чана только через первый кран длится вдвое дольше, чем через второй кран. За какой промежуток времени каждый кран, работая отдельно, может наполнить чан?
Задание № 7.25. Аквариум объёмом 54 м3 заполняется при помощи двух кранов. При этом первый кран работает 3 ч, а второй — 2 ч. Какова пропускная способность первого крана, если 1 м3 он заполняет на 1 мин медленнее, чем второй?
Задание № 7.26. Два тракториста, работая совместно, вспахали поле за 48 ч. Если бы половину поля вспахал один из них, а затем оставшуюся половину другой, то работа была бы выполнена за 100 ч. За сколько часов мог бы вспахать поле каждый тракторист, работая отдельно?
Задание № 7.27. Двое рабочих вместе могут справиться с заданием за 2 ч. Если один из них сделает 40% задания, а затем второй — оставшуюся часть работы, то на выполнение задания понадобится 4 ч. За какое время сможет выполнить всё задание каждый рабочий, действуя в одиночку, если известно, что производительность труда у них различная?
Задание № 7.28. Сумма квадратов цифр двузначного числа равна 13. Если от этого числа отнять 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите исходное число.
Задание № 7.29. Если задуманное двузначное число умножить на цифру его единиц, то получится 376, а если из задуманного числа вычесть двузначное число, записанное теми же цифрами, но в обратном порядке, то получится 45. Какое число задумано?
Задание № 7.30. Задуманы два натуральных числа, произведение которых равно 720. Если первое число разделить на второе, то в частном получится 3 и в остатке 3. Какие числа задуманы?
Задание № 7.31. При перемножении двух натуральных чисел, разность которых равна 7, была допущена ошибка: цифра сотен в произведении увеличена на 4. При делении полученного (неверного) произведения на меньший множитель получилось в частном 52 и в остатке 26. Найдите исходные числа.
Задание № 7.32. Если двузначное число разделить на сумму его цифр, то в частном получится 7 и в остатке 6. Если это же двузначное число разделить на произведение его цифр, то в частном получится 3, а в остатке число, равное сумме цифр исходного числа. Найдите исходное число.
Задание № 7.33. На участке одноколейной железной дороги длиной 10 км надо уложить рельсы (две полосы). Для укладки имеются рельсы длиной 25 м и 12,5 м. Если уложить все рельсы длиной 25 м, то надо будет израсходовать половину имеющегося количества рельсов длиной 12,5 м. Если же уложить все имеющиеся рельсы длиной 12,5 м, то рельсов длиной 25 м надо уложить 2/3 их количества. Определите общее количество имеющихся рельсов.
Задание № 7.34. Велосипедист за каждую минуту проезжает на 600 м меньше, чем мотоциклист, поэтому на путь длиной 120 км он затрачивает времени на 3 ч больше, чем мотоциклист. Найдите скорости велосипедиста и мотоциклиста.
Задание № 7.35. Автомобили двух моделей выехали из пунктов А и В навстречу друг другу, причём автомобиль первой модели вышел из А на 15 с раньше. Пройдя расстояние АВ, равное 60 м, каждый сразу повернул обратно и вернулся к месту старта. Найдите скорость каждого автомобиля, если первая встреча между ними произошла через 21 с, а вторая — через 45 с после выхода автомобиля первой модели.
Задание № 7.36. Из пункта А в одном и том же направлении вышли два лыжника, причём второй стартовал на 6 мин позже первого и догнал первого в 3 км от старта. Дойдя до отметки 5 км, второй лыжник повернул обратно и встретил первого в 4,6 км от старта. Найдите скорости лыжников.
Задание № 7.37. Из пункта А в пункт В, находящийся на расстоянии 70 км от пункта А, выехал велосипедист, а через некоторое время — мотоциклист со скоростью движения 50 км/ч. Мотоциклист догнал велосипедиста в 20 км от пункта А. Прибыв в В, мотоциклист через 36 мин выехал обратно и встретился с велосипедистом спустя 3 ч 20 мин после выезда велосипедиста из А. Найдите скорость велосипедиста.
Задание № 7.38. Два пешехода вышли одновременно навстречу друг другу из пунктов А и В. Каждый идёт с постоянной скоростью без остановок и, придя в конечный пункт, тут же поворачивает обратно. Когда пешеходы встретились во второй раз, оказалось, что первый прошёл на 4 км больше, чем второй. После второй встречи первый прибыл в А через час, а второй в В — через 2,5 ч. Найдите скорости пешеходов.
Задание № 7.39. Два поезда отправляются из пунктов А и В навстречу друг другу. Если поезд из А выйдет на 2 ч раньше, чем поезд из B, то встреча произойдёт на середине пути. Если поезда выйдут одновременно, то они встретятся через 3 ч 45 мин. Найдите скорость поездов и расстояние между А и B, если известно, что скорость одного поезда на 40 км/ч больше скорости другого.
Задание № 7.40. По окружности длиной 60 м равномерно в одном направлении движутся две точки. Одна из них совершает полный оборот на 5 с быстрее другой. При этом совпадение точек происходит каждый раз через 1 мин. Определите скорости движения точек.
Задание № 7.41. Турист проплыл по реке на лодке 90 км и прошёл пешком 10 км. При этом на пеший путь было затрачено на 4 ч меньше, чем на путь по реке. Если бы турист шёл пешком столько времени, сколько на самом деле он плыл по реке, а плыл по реке столько времени, сколько на самом деле шёл пешком, то соответствующие расстояния были бы равны. Сколько времени он шёл пешком и сколько времени он плыл по реке?
Задание № 7.42. От пристани А одновременно отправились вниз по течению катер и плот. Катер прошёл 96 км, затем повернул обратно и вернулся к пристани А через 14 ч. Известно, что скорость катера по течению в 1 1/3 раза больше скорости катера против течения. На каком расстоянии от пристани А катер встретил плот на обратном пути?
Задание № 7.43. Две наборщицы напечатали текст рукописи за 6 ч. Если сначала первая наборщица напечатает половину рукописи, а затем вторая — оставшуюся часть, то на всю работу будет затрачено 12,5 ч. За какое время может выполнить всю работу каждая наборщица?
Задание № 7.44. Бригада слесарей может выполнить некоторое задание по обработке деталей на 15 ч скорее, чем бригада учеников. Если бригада учеников отработает 18 ч, выполняя это задание, а потом бригада слесарей продолжит выполнение задания в течение 6 ч, то будет выполнено только 60% всего задания. Сколько времени требуется бригаде учеников для самостоятельного выполнения задания?
Задание № 7.45. Мастер, работая с учеником, обрабатывает деталь за 2 ч 24 мин. Если мастер будет работать 2 ч, а ученик — 1 ч, то будет выполнено 2/3 всей работы. Сколько времени потребуется мастеру и ученику в отдельности на обработку детали?
Задание № 7.46. Две бригады, работая вместе, должны отремонтировать участок шоссейной дороги за 18 дней. В действительности же получилось так, что сначала работала первая бригада, а заканчивала ремонт участка дороги вторая бригада, работающая не более чем в два раза быстрее первой. В результате ремонт участка дороги продолжался 40 дней, причём первая бригада в своё рабочее время выполнила 2/3 всей работы. За сколько дней был бы отремонтирован участок дороги каждой бригадой отдельно?
Задание № 7.47. В бассейн проведены две трубы разного сечения. Одна равномерно подаёт, а вторая равномерно отводит воду, причём через первую бассейн наполняется на 2 ч дольше, чем через вторую опорожняется. При заполненном на 1/3 бассейне были открыты обе трубы, и бассейн оказался пустым спустя 8 ч. За сколько часов, действуя отдельно, первая труба наполняет, а вторая опорожняет бассейн?
Задание № 7.48. По двум сторонам прямого угла по направлению к его вершине движутся два тела. В начальный момент тело А отстояло от вершины на 60 м, а тело В — на 80 м. Через 3 с расстояние между А и В стало равным 70 м, а ещё через 2 с — 50 м. Найдите скорость движения каждого тела.
Задание № 7.49. В январе 2014 г. на счёт в банке была положена некоторая сумма денег. В конце 2014 г. проценты по вкладу составили 2000 р. Добавив в январе 2015 г. на свой счёт ещё 18000 р., вкладчик пришёл в банк закрыть счёт в декабре 2015 г. и получил 44000 р. Какая сумма была положена на счёт первоначально и сколько процентов в год начисляет банк?
Задание № 7.50. У старшего брата было вдвое больше денег, чем у младшего. Они положили свои деньги на год на счета в разные банки, причём младший брат нашёл банк, который даёт на 5 % годовых больше, чем банк, в который обратился старший брат. Сняв свои деньги со счетов через год, старший брат получил 4600 р., а младший — 2400 р. Сколько денег было бы у братьев в сумме, если бы они с самого начала поменяли свои банки?
Задание № 7.51. Суммарный доход двух предприятий возрастёт втрое, если доход первого предприятия останется неизменным, а доход второго увеличится в 4 раза. Во сколько раз надо увеличить доход первого предприятия, оставляя неизменным доход второго, чтобы их суммарный доход вырос в 4 раза?
Задание № 7.52. Торговая фирма получила две партии некоторого товара. Если продавать весь товар по цене 80 р. за 1 кг, то выручка от продаж будет на 15 % ниже выручки, которую фирма получила бы, продав первую партию по названной цене, а вторую — по цене, превышающей её на 25%. Какую часть (по массе) составляет первая партия товара в общем количестве товара этих двух партий?
Задание № 7.53. При смешивании 40%-ного раствора соли с 10%-ным раствором получили 800 г раствора с концентрацией соли 21,25%. Сколько граммов каждого раствора было для этого взято?
Задание № 7.54. Имеются два раствора соли в воде, первый — 40%-ный, второй — 60%-ный. Их смешали, добавили 5 л воды и получили 20%-ный раствор. Если бы вместо 5 л воды добавили 5л 80%-ного раствора соли, то получился бы 70%-ный раствор. Сколько было 40%-ного и сколько 60%-ного раствора?
Задание № 7.55. Имеется три слитка. Масса первого равна 5 кг, масса второго 3 кг, и каждый из них содержит 30 % меди. Если первый слиток сплавить с третьим, то получится слиток, содержащий 56% меди. Если второй слиток сплавить с третьим, то получится слиток, содержащий 60% меди. Каким будет процентное содержание меди в сплаве из всех трёх слитков?
Вы смотрели: ГДЗ Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ГЛАВА 2. СИСТЕМЫ УРАВНЕНИЙ. § 7. Системы уравнений как математические модели реальных ситуаций. ОТВЕТЫ на задачи 7.23 — 7.55.