ГДЗ Алгебра 9 класс Мордкович. Решения и ответы на Контрольную работу № 1 (4 варианта). Цитаты из пособия указаны в учебных целях. Ответы на контрольные работы адресованы родителям.
Вернуться к списку контрольных (в ОГЛАВЛЕНИЕ)
Алгебра Мордкович. Контрольная работа 1
К-1 Вариант 1 (задания)

РЕШЕНИЯ и ОТВЕТЫ на Вариант 1
К-1 Вариант 2 (задания)

РЕШЕНИЯ и ОТВЕТЫ на Вариант 2
К-1 Вариант 3 (задания)

РЕШЕНИЯ и ОТВЕТЫ на Вариант 3
К-1 Вариант 4 (задания)

РЕШЕНИЯ и ОТВЕТЫ на Вариант 4
ГДЗ Алгебра 9 класс Мордкович. Решения и ответы на Контрольную работу № 1. Цитаты из пособия указаны в учебных целях. Ответы на контрольные работы адресованы родителям.
Вернуться к списку контрольных (в ОГЛАВЛЕНИЕ)
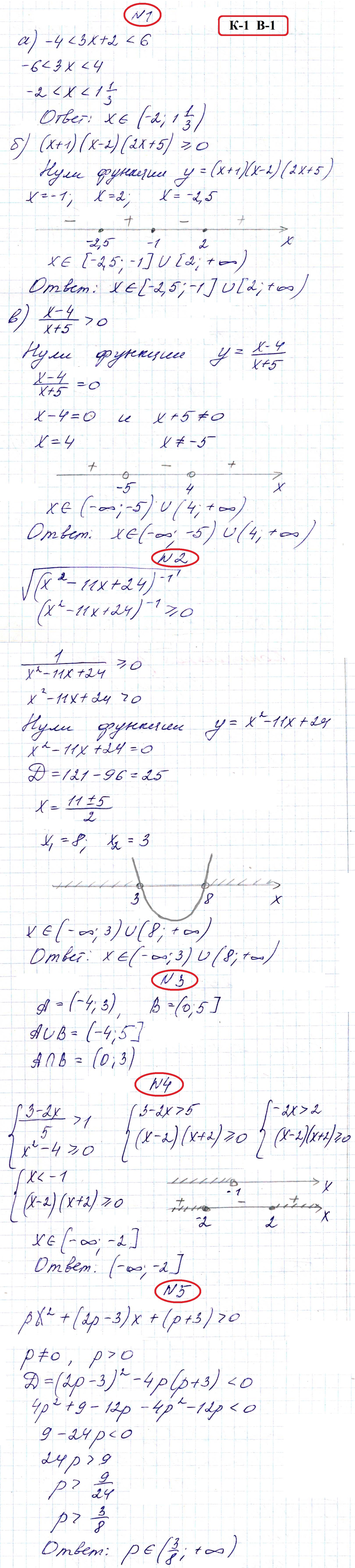
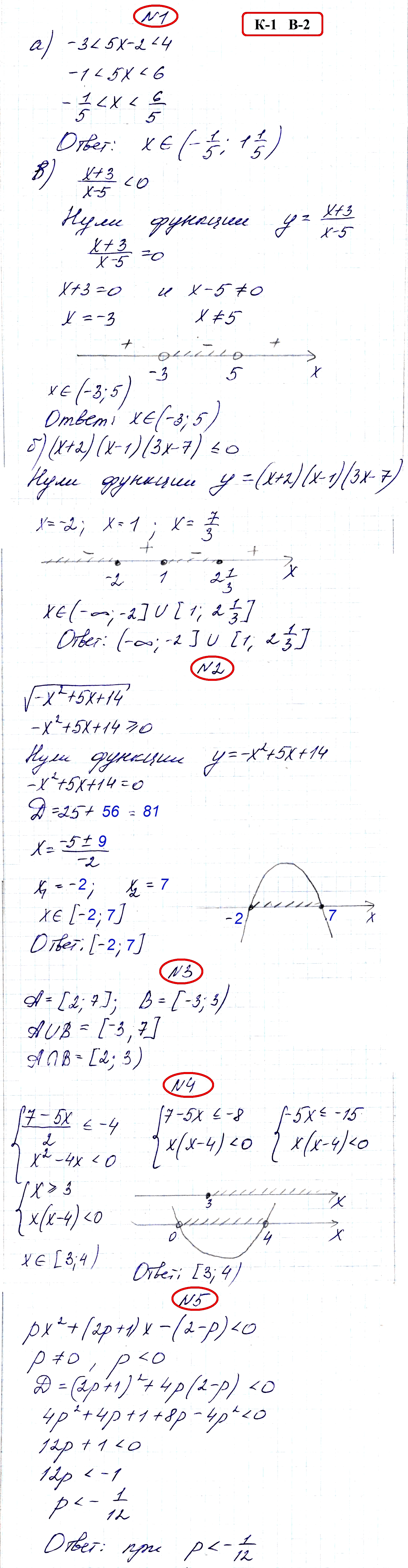


Во втором варианте, в номере 2 ошибка. Не 96, а 56
Исправлено. Спасибо.
Добрый день. Разместите условия вариантов 3 и 4. Спасибо
Добавили.