Конспект по физике для 9 класса «Движение тела, брошенного горизонтально». Как движется тело, брошенное горизонтально. Как найти дальность и высоту полёта тела, брошенного горизонтально. Как найти модуль скорости тела, брошенного горизонтально.
Конспекты по физике Учебник физики Тесты по физике
Движение тела,
брошенного горизонтально
Мы рассмотрели самые простые случаи движения тела под действием силы тяжести: свободное падение и движение тела, брошенного вертикально вверх. Теперь рассмотрим случай, когда тело, движущееся под действием силы тяжести, имеет начальную скорость, направленную горизонтально. Примерами такого движения могут быть: движение мяча, брошенного горизонтально; движение стрелы, выпущенной из лука горизонтально, и т. п.
ПРИНЦИП СЛОЖЕНИЯ ДВИЖЕНИИ
До сих пор мы рассматривали только прямолинейное движение, для описания которого было достаточно одной координатной оси. При этом сила тяжести, действующая на тело, была параллельна этой оси.
Пусть шарик движется без трения по горизонтальной поверхности со скоростью ʋ0. Согласно первому закону Ньютона в горизонтальном направлении никакие силы на шарик не действуют (он движется равномерно). При движении по плоскости сила тяжести, действующая на шарик, компенсируется силой реакции опоры, т. е. равнодействующая этих сил равна нулю. В момент, когда шарик достигает края горизонтальной поверхности, сила реакции опоры исчезает. При этом в горизонтальном направлении шарик продолжает своё движение по инерции с той же скоростью ʋ0. А в вертикальном направлении на него теперь действует только сила тяжести (силой сопротивления воздуха мы пренебрегаем), поэтому он начинает равноускоренное движение вниз с ускорением свободного падения g.
Таким образом, движение шарика можно представить как сложение двух независимых движений: движения вдоль горизонтальной оси ОХ и движения вдоль вертикальной оси OY.
Изучением движения тел, брошенных горизонтально, занимался Галилей. В своих трудах этот вид движения он описал как сумму двух движений: по горизонтали и по вертикали, введя тем самым в механику принцип сложения движений.
ТРАЕКТОРИЯ ДВИЖЕНИЯ ТЕЛА, БРОШЕННОГО ГОРИЗОНТАЛЬНО
Рассмотрим движение тела, брошенного с высоты h0 и имеющего начальную скорость ʋ0. Для описания этого движения направим координатную ось ОХ горизонтально, а ось ОY направим вертикально вверх. Траектория этого движения имеет вид плавной кривой, называемой параболой. Движение, при котором траектория не является прямой линией, называют криволинейным.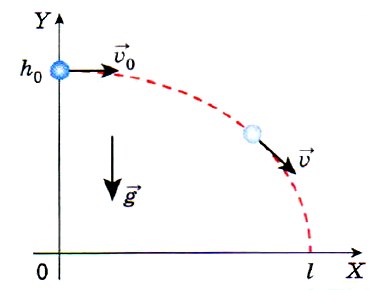
ДВИЖЕНИЕ ВДОЛЬ ВЕРТИКАЛЬНОЙ ОСИ
Проекция ускорения свободного падения на ось OY отрицательна и равна gy = -g. Направление начальной скорости ʋ0 совпадает с направлением оси ОХ, поэтому ʋ0у = 0.
Поскольку скорость тела, движущегося равноускоренно, в момент времени t можно найти по формуле![]()
Найдём высоту h, на которой находится тело в момент времени t. Для этого воспользуемся уравнением движения тела: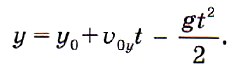
Обозначим начальную высоту у0 как h0. Получим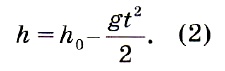
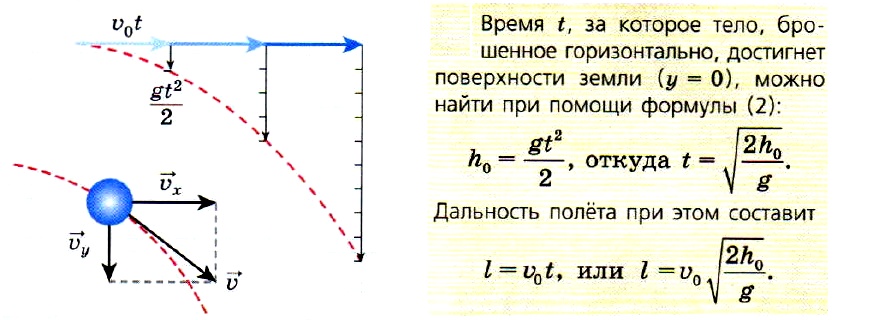
Проведём на листе клетчатой бумаги вертикальную и горизонтальную линии. Так как движения в горизонтальном и вертикальном направлениях происходят независимо друг от друга, то через время t с тело переместится на отрезок ʋ0t вправо и на отрезок gt2/2 вниз. Если отложить по горизонтали отрезок ʋ0t, а из его конца вертикальный отрезок gt2/2, то получится точка, в которой тело окажется через t с. Сделав подобное построение для нескольких промежутков времени и соединив эти точки плавной линией, получим ветвь параболы.
СКОРОСТЬ ТЕЛА, БРОШЕННОГО ГОРИЗОНТАЛЬНО
Мы уже знаем, что движение тела, брошенного горизонтально, можно рассматривать как сложение движений вдоль горизонтальной и вертикальной осей. В каждый момент времени такое тело имеет мгновенную скорость ʋ, проекции которой можно найти по формулам (1) и (3).
Если обозначить скорость движения тела вдоль оси ОХ через ʋx, а его скорость вдоль оси OY через ʋу, то можно записать:![]() т. е. вектор скорости тела можно найти как сумму векторов скоростей тела вдоль осей.
т. е. вектор скорости тела можно найти как сумму векторов скоростей тела вдоль осей.
Для того чтобы изобразить вектор, являющийся суммой двух векторов, используют правило параллелограмма: для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
В нашем случае векторы ʋx и ʋу перпендикулярны друг другу, поэтому их сумма — диагональ прямоугольника. Значение (модуль) скорости тела в любой момент времени можно найти по теореме Пифагора: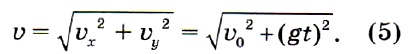
Вы смотрели Конспект по физике для 9 класса «Движение тела, брошенного горизонтально».
Вернуться к Списку конспектов по физике (Оглавление).