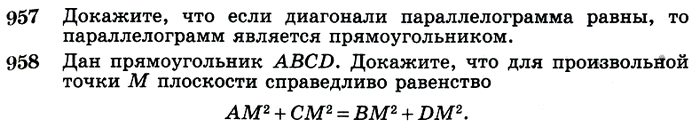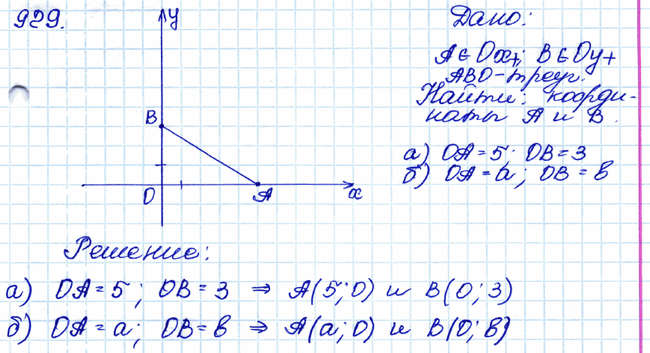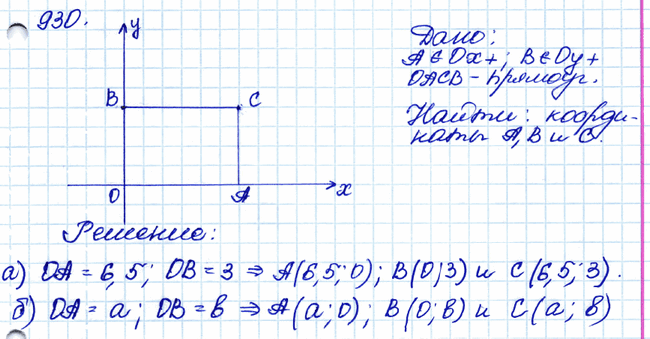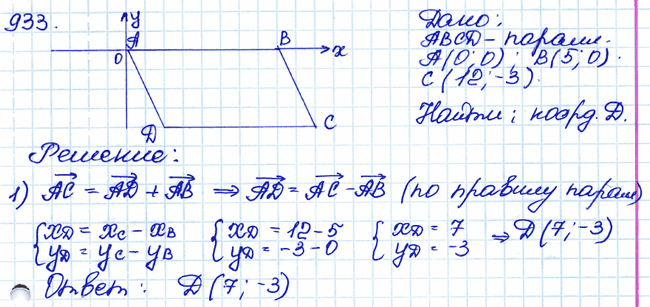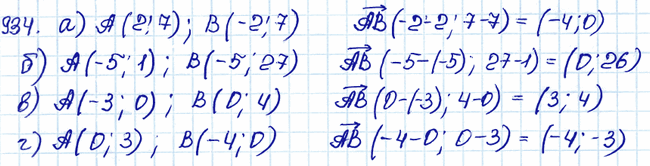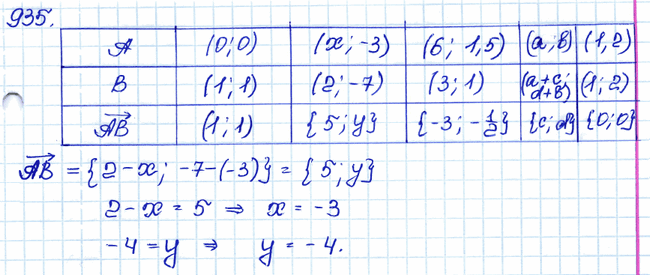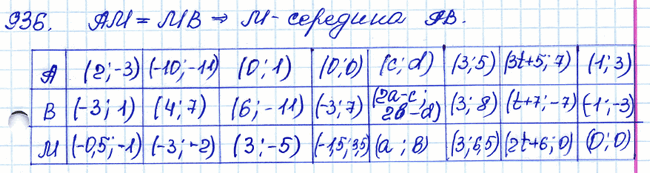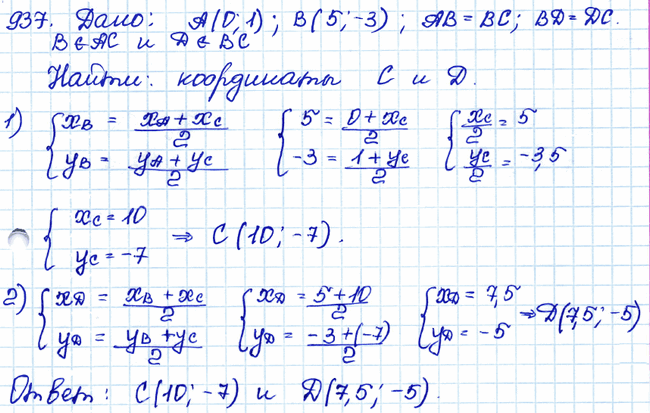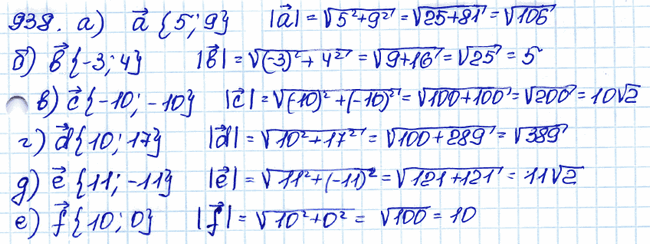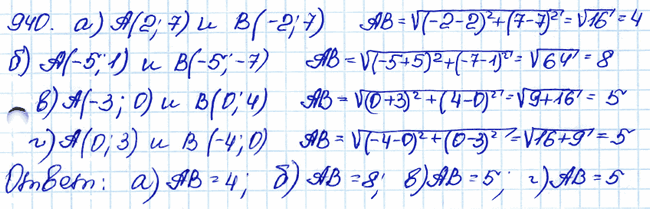Геометрия 9 класс УМК Атанасян, Бутузов и др. Задачи №№ 929 — 958 из учебника с ответами и решениями. Глава X. Метод координат. § 2. Простейшие задачи в координатах (91. Связь между координатами вектора и координатами его начала и конца. 92. Простейшие задачи в координатах). Геометрия Атанасян Задачи 929-958 + ОТВЕТЫ.
О Г Л А В Л Е Н И Е Вернуться к списку тем учебника
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия 9 класс (Атанасян)
Глава X. Задачи 929 — 958
Задача № 929. □ Точка А лежит на положительной полуоси Ох, а точка В — на положительной полуоси Оу. Найдите координаты вершин треугольника АВО, если: а) ОА = 5, ОВ = 3; б) ОА = а, ОВ = b.
Задача № 930. □ Точка А лежит на положительной полуоси Ох, а точка В — на положительной полуоси Оу. Найдите координаты вершин прямоугольника ОАСВ, если: а) ОА = 6,5, ОВ = 3; б) ОА = а, ОВ = b.
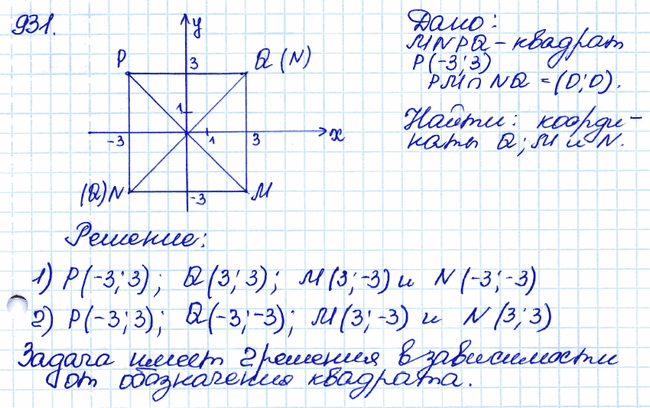
Задача № 931. Начертите квадрат MNPQ так, чтобы вершина Р имела координаты (–3; 3), а диагонали квадрата пересекались в начале координат. Найдите координаты точек М, N и Q. .
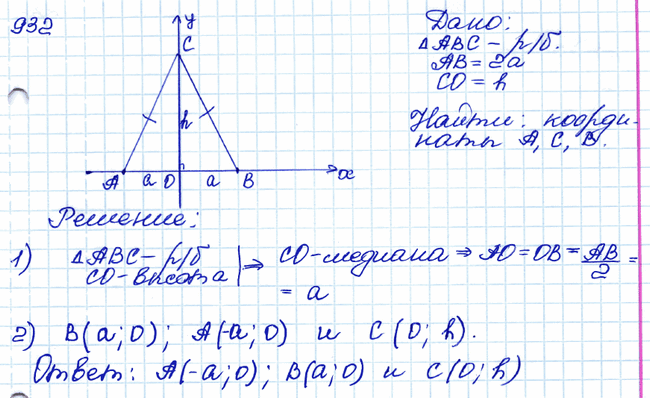
Задача № 932. Найдите координаты вершин равнобедренного треугольника АВС, изображённого на рисунке 281, если АВ = 2а, а высота СО рис 281 равна h. .
Задача № 933. □ Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; –3.). .
Задача № 934. □ Найдите координаты вектора АВ, зная координаты его начала и конца: а) А (2; 7), В (–2; 7); б) А (–5; 1), В (–5; 27); в) А (–3; 0), В (0; 4); г) А (0; 3), В (–4; 0). .
Задача № 935. □ Перечертите таблицу в тетрадь, заполните пустые клетки и найдите х и у:
| А | (0; 0) | (x; –3) | (а, b) | (1; 2) | |
| В | (1; 1) | (2; –7) | (3; 1) | ||
| АВ | {5; у} | {–3; –1/2} | {с; d} | {0; 0} |
Задача № 936. □ Перечертите таблицу в тетрадь и, используя формулы для вычисления координат середины М отрезка АВ, заполните пустые клетки:
| А | (2; –3) | (0; 1) | (0; 0) | (с; d) | (3; 5) | (3t + 5; 7) | (1; 3) | |
| В | (–3; 1) | (4; 7) | (–3; 7) | (3; 8) | (t + 7; –7) | |||
| M | (–3; –2) | (3; –5) | (а; b) | (0; 0) |
Задача № 937. □ Даны точки А (0; 1) и B (5; –3). Найдите координаты точек С и D, если известно, что точка B — середина отрезка АС, а точка D — середина отрезка ВС. .
Задача № 938. □ Найдите длины векторов: а) а {5; 9}; б) b {–3; 4}; в) с {–10; –10}; г) d {10; 17}; д) е {11; –11}; е) f {10; 0}. .
Задача № 939. □ Найдите расстояние от точки М (3; –2): а) до оси абсцисс; б) до оси ординат; в) до начала координат. .
Задача № 940. □ Найдите расстояние между точками А и Б, если: а) А (2; 7), B (–2; 7); б) А (–5; 1), B (–5; –7); в) А (–3; 0), B (0; 4); г) А (0; 3), B (–4;0). .
Задача № 941. □ Найдите периметр треугольника MNP, если М (4; 0), N (12; –2), P (5;–9). .
Задача № 942. □ Найдите медиану AM треугольника АВС, вершины которого имеют координаты: А (0; 1), В (1; –4), С (5; 2). .
Задача № 943. Точки B и С лежат соответственно на положительных полуосях Ох и Оу, а точка А лежит на отрицательной полуоси Ох, причём ОА = а, OB = b, OC = h. Найдите стороны АС и ВС треугольника АВС. .
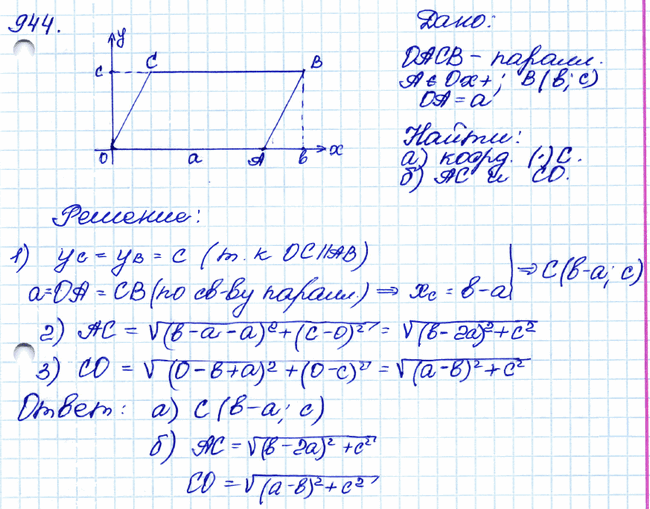
Задача № 944. Вершина А параллелограмма ОАСВ лежит на положительной полуоси Ох, вершина В имеет координаты (b; с), а ОА = а. Найдите: а) координаты вершины С; б) сторону АС и диагональ СО. .
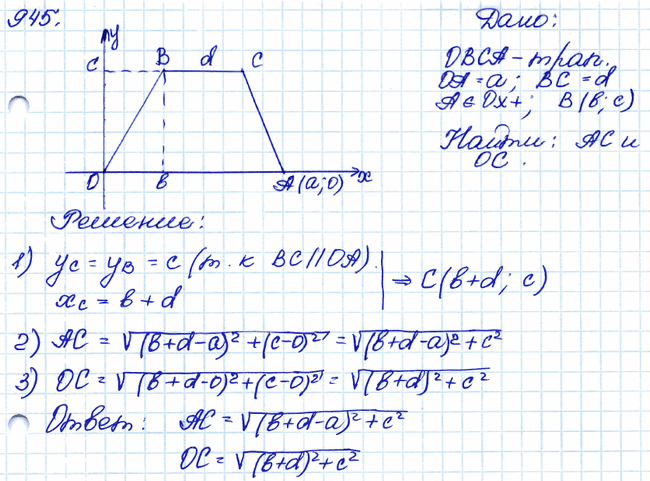
Задача № 945. Найдите сторону АС и диагональ ОС трапеции ОВСА с основаниями ОА = а и ВС = d, если точка А лежит на положительной полуоси Ох, а вершина В имеет координаты (b; с). .
Задача № 946. Найдите х, если: а) расстояние между точками А (2; 3) и В (х; 1) равно 2; б) расстояние между точками М1 (–1; х) и М2 (2х; 3) равно 7. .
Задача № 947. Докажите, что треугольник АВС равнобедренный, и найдите его площадь, если вершины треугольника имеют координаты: а) А (0; 1), В (1; –4), С (5; 2); б) А (–4; 1), В (–2; 4), С (0; 1). .
Задача № 948. На оси ординат найдите точку, равноудалённую от точек: а) А (–3; 5) и B (6; 4); б) С (4; –3) и D (8; 1). .
Задача № 949. На оси абсцисс найдите точку, равноудалённую от точек: а) А (1; 2) и B (–3; 4); б) С (1; 1) и D (3; 5). .
Задача № 950. Докажите, что четырёхугольник MNPQ является параллелограммом, и найдите его диагонали, если: а) М (1; 1), N (6; 1), P (7; 4), Q (2; 4); б) М (–5; 1), N (–4; 4), Р (–1; 5), Q(–2; 2). .
Задача № 951. Докажите, что четырёхугольник ABCD является прямоугольником, и найдите его площадь, если: а) А (–3; –1), B (1; –1), С (1; –3), D (–3; –3); б) А (4; 1), B (3; 5), С (–1; 4), D (0; 0). .
Задача № 952. Докажите, что середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин. .
Задача № 953. Докажите, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей. .
Задача № 954. Медиана, проведённая к основанию равнобедренного треугольника, равна 160 см, а основание треугольника равно 80 см. Найдите две другие медианы этого треугольника. .
Задача № 955. Высота треугольника, равная 10 см, делит основание на два отрезка, равные 10 см и 4 см. Найдите медиану, проведённую к меньшей из двух других сторон. .
Задача № 956. Докажите, что в равнобедренной трапеции диагонали равны. Сформулируйте и докажите обратное утверждение. .
Задача № 957. Докажите, что если диагонали параллелограмма равны, то параллелограмм является прямоугольником. .
Задача № 958. Дан прямоугольник ABCD. Докажите, что для произвольной точки М плоскости справедливо равенство AM2 + СМ2 = ВМ2 + DM2. .
Вы смотрели: Геометрия 9 класс УМК Атанасян, Бутузов и др. Задачи №№ 929 — 958 из учебника с ответами и решениями. § 2. Простейшие задачи в координатах (91. Связь между координатами вектора и координатами его начала и конца. 92. Простейшие задачи в координатах). Геометрия Атанасян Задачи 929-958 + ОТВЕТЫ.