Конспект по физике для 9 класса «Период и частота». Что такое период обращения. Что такое частота обращения. Как вычислить скорость и ускорение тела, движущегося по окружности, если известны его период и частота обращения.
Конспекты по физике Учебник физики Тесты по физике
Период и частота
Измерить скорость тела, движущегося по окружности, не всегда просто. Однако её можно вычислить, используя такие понятия, как период и частота обращения.
ПЕРИОД
Когда тело движется по окружности с постоянной по модулю скоростью, через определённые промежутки времени движение повторяется снова и снова. Примером этому может служить движение на обычной детской карусели.
Время, в течение которого тело совершает один полный оборот, называют периодом обращения. Период обращения принято обозначать буквой Т. Единица этой физической величины в СИ — секунда.
С понятием периода обращения вы уже знакомились при изучении географии. Например, период обращения Земли вокруг своей оси составляет 23 ч 56 мин 4 с, а период обращения Земли вокруг Солнца — 1,00004 земных года. Самый короткий период обращения вокруг Солнца в нашей Солнечной системе имеет планета Меркурий. Её период обращения составляет 0,24085 земных лет. Интересно, что самая большая планета Солнечной системы — Юпитер — имеет самый короткий период обращения вокруг своей оси — всего 9 ч 50 мин. В 226 000 000 лет оценивается период обращения Солнечной системы вокруг ядра Галактики.
ЧАСТОТА
Число оборотов в единицу времени, которое совершает тело при движении по окружности, называют частотой обращения. Частоту обращения обозначают греческой буквой ν.
Если, катаясь на карусели в парке, мы совершаем один оборот за 20 с, то период обращения в этом случае Т = 20 с. Как определить частоту обращения при этом движении? Сколько оборотов совершает карусель за 1 с?
Очевидно, ν = 1/Т = 1/20 1/с, т. е. за 1 с карусель совершает одну двадцатую часть своего полного оборота.
Таким образом, частота обращения является величиной, обратной периоду обращения:
Именно поэтому единица этой физической величины обратна секунде, т. е. 1/с, или с-1.
СВЯЗЬ МОДУЛЯ СКОРОСТИ С ПЕРИОДОМ И ЧАСТОТОЙ ОБРАЩЕНИЯ
Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности R и период или частоту обращения. Действительно, один полный оборот тело совершает за время, равное периоду обращения Т. Путь, пройденный телом, в этом случае равен длине окружности: l = 2πR. Тогда можно записать:
или с учётом формулы (1):![]()
С учётом формул (2) и (3) можно найти центростремительное ускорение тела, выразив скорость через период или частоту обращения: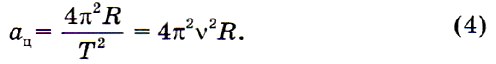
Часто мгновенную скорость движения по окружности называют линейной скоростью.
Модуль скорости движения тела по окружности рассчитывается по формуле: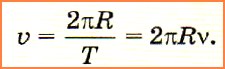
Умение описывать движение тела по окружности чрезвычайно важно, так как движение по криволинейной траектории можно приближённо представить как движение по дугам окружностей различных радиусов.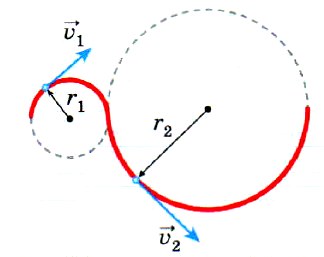
РЕШЕНИЕ ЗАДАЧ
Задача 1. Найдём модуль скорости вращения ребёнка на карусели, если радиус окружности, по которой происходит движение, равен 2,3 м, а время, за которое карусель совершает один полный оборот, равно 20 с.
Ответ: υ = 0,722 м/с.
Задача 2. Земля делает один оборот вокруг Солнца за 365 дней. Расстояние от Солнца до Земли составляет 149,6 • 106 км. Определим линейную скорость движения Земли вокруг Солнца, считая орбиту окружностью.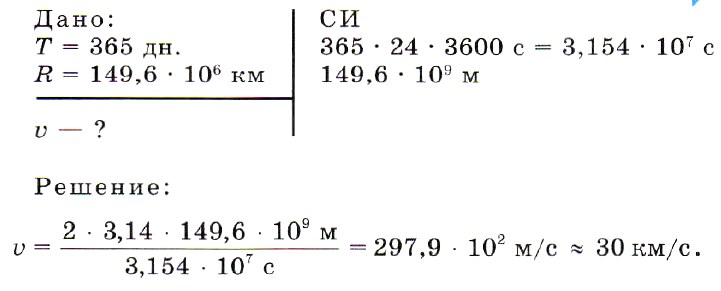
Ответ: υ ≈ 30 км/с.
Вы смотрели Конспект по физике для 9 класса «Период и частота».
Вернуться к Списку конспектов по физике (Оглавление).