Частная школа. 9 класс

Конспект по физике для 9 класса «Движение тела по окружности». Куда направлена мгновенная скорость тела при его движении по окружности. Куда направлено ускорение тела при его движении по окружности и как вычислить его значение.

Конспекты по физике    Учебник физики    Тесты по физике

---

Движение тела по окружности

Одним из простейших видов криволинейного движения является движение тела по окружности. Рассмотрим такое движение при постоянной по модулю скорости.

Согласно второму закону Ньютона направление ускорения совпадает с направлением равнодействующей всех сил, действующих на тело. Сообщим шарику, лежащему на столе и закреплённому на нити, начальную скорость в направлении, перпендикулярном нити. Он начнёт двигаться по окружности. Сила тяжести, действующая на него, уравновешивается силой упругости стола, а сила трения качения мала, и ею можно пренебречь. Получается, что сила, обусловливающая движение шарика по окружности, — сила упругости нити, направленная по радиусу окружности. Поэтому ускорение должно быть направлено так же, т. е.по радиусу окружности в направлении к центру.

НАПРАВЛЕНИЕ ВЕКТОРА МГНОВЕННОЙ СКОРОСТИ

При движении тела по окружности при неизменном модуле скорости в каждый момент времени скорость меняет своё направление. Как направлен вектор мгновенной скорости?

Для ответа на этот вопрос представим себе движение некоторого тела, закреплённого на верёвке и раскрученного в горизонтальной плоскости.

Если верёвка оборвётся, то тело начнёт двигаться по прямой. Эта прямая — касательная к окружности, являющейся траекторией движения тела. При этом направление движения тела совпадает с направлением скорости тела в момент разрыва верёвки.

Таким образом, мгновенная скорость тела в любой точке траектории направлена по касательной к траектории в этой точке.

НАПРАВЛЕНИЕ ВЕКТОРА УСКОРЕНИЯ ТЕЛА, ДВИЖУЩЕГОСЯ ПО ОКРУЖНОСТИ

При движении по окружности с постоянной по модулю скоростью в каждый момент времени направление скорости изменяется. Значит, такое движение является движением с ускорением. Рассмотрим движение тела по окружности радиуса R. Обозначим скорость тела в точке А через ʋ₁, а его скорость в точке В через ʋ₂. Тогда ускорение, с которым тело движется, можно найти по формуле

В числителе этой формулы стоит векторная физическая величина, а в знаменателе — скалярная. Поэтому направление вектора ускорения должно совпадать с направлением вектора, равного разности векторов скоростей:

Для того чтобы изобразить вектор, являющийся разностью двух векторов, используют правило треугольника. Сначала векторы изображают исходящими из одной точки (при этом перемещать их можно только при помощи параллельного переноса). Затем проводят отрезок так, чтобы получился треугольник.

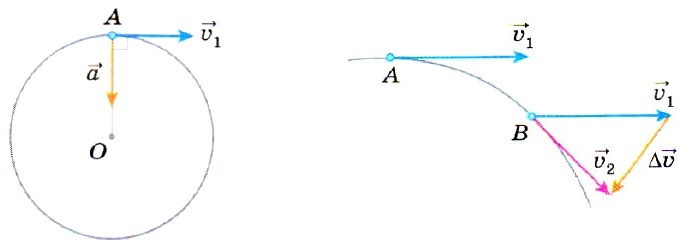
В нашем случае направленный отрезок, соединяющий конец вычитаемого вектора ʋ₁ с концом уменьшаемого вектора ʋ₂, и будет их векторной разностью.

Из рисунка видно, что вектор Δʋ и, следовательно, вектор a направлены внутрь окружности. Для того чтобы понять, как направлено ускорение в определённой точке траектории представим, что промежуток времени от момента нахождения тела в точке А до момента, когда тело стало находиться в точке В, становится всё меньше и меньше. Тогда точки А и В стягиваются в одну точку А. При этом направление вектора Δʋ приближается к направлению вектора AO.

Получается, что ускорение тела, движущегося по окружности с постоянной по модулю скоростью, направлено по радиусу окружности к её центру. Именно поэтому оно называется центростремительным и обозначается а_ц.

Так как касательная к окружности перпендикулярна радиусу, проведённому в точке касания, то векторы скорости ʋ и центростремительного ускорения а_ц перпендикулярны друг другу.

МОДУЛЬ ЦЕНТРОСТРЕМИТЕЛЬНОГО УСКОРЕНИЯ ТЕЛА

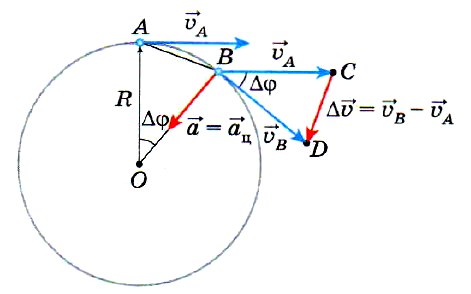
Для нахождения модуля центростремительного ускорения вновь обратимся к рисунку.

---

Вы смотрели Конспект по физике для 9 класса «Движение тела по окружности».

Вернуться к Списку конспектов по физике (Оглавление).