Конспект по физике для 9 класса «Период колебаний математического маятника». От чего зависит период колебаний математического маятника. Как вычислить период колебаний математического маятника.
Конспекты по физике Учебник физики Тесты по физике
Период колебаний
математического маятника
Наблюдая в Пизанском соборе за качанием подвешенной на длинной цепи центральной люстры со свечами (паникадила), которую толкнули при зажигании свечей, Галилей обратил внимание на то, что амплитуда колебаний постепенно уменьшалась, но период оставался одним и тем же.
ЗАКОНОМЕРНОСТИ КОЛЕБАНИЙ МАТЕМАТИЧЕСКОГО МАЯТНИКА
Можно считать, что в соборе Галилей наблюдал за колебательной системой, которую приближённо можно считать математическим маятником. Интересно то, что период колебаний Галилей определял, пользуясь собственным пульсом. Эти наблюдения побудили Галилея приступить к исследованиям, результаты которых имели огромное теоретическое и практическое значение.
Наблюдения и опыты с математическим маятником позволили установить две закономерности:
- Если отклонять маятник на различные (но не слишком большие) углы и затем отпускать, то он будет колебаться с одинаковым периодом, хотя и с разными амплитудами, т. е. период колебаний маятника не зависит от амплитуды.
- Если при одной и той же длине маятника подвешивать грузы различной массы, период колебаний будет один и тот же. Следовательно, период колебаний маятника не зависит от массы груза.
Можно оценить, сколько ударов пульса мог отсчитать Галилей за один период колебаний, если известно, что длина цепи, на которой была подвешена люстра в Пизанском соборе, приблизительно составляет 49 м. Оценки показывают, что период колебаний такого маятника составляет около 14 с. Если предположить, что сердце бьётся с частотой 60 ударов в минуту, то это число составит 14 ударов.
ФОРМУЛА ПЕРИОДА МАТЕМАТИЧЕСКОГО МАЯТНИКА
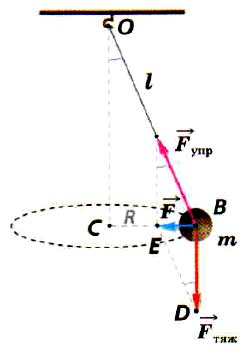
При колебании маятника в вертикальной плоскости груз движется ускоренно по дуге под действием равнодействующей силы F, которая меняется при движении.
Таким образом, мы наблюдаем ускоренное движение, при котором ускорение меняется с течением времени. Для количественного описания такого движения элементарных знаний механики и математики уже недостаточно. Поэтому для упрощения мы поступим следующим образом.
Предположим, что маятник колеблется так, чтобы нить маятника описывала конус и груз двигался по окружности.
Период обращения маятника по конусу и период колебания в одной плоскости будут близки. При этом чем меньше угол отклонения, тем ближе будут значения периодов. Поэтому для вывода формулы периода колебаний математического маятника можно воспользоваться результатом, полученным для конического маятника. Для этого надо взять два одинаковых маятника и заставить один из них колебаться в вертикальной плоскости, а другой вращаться по конусу. Период обращения маятника по конусу будет таким же, что и период колебания в одной плоскости. Период обращения конического маятника равен отношению длины описываемой грузом окружности к значению его скорости: Если угол отклонения невелик, то можно считать, что сила F направлена по радиусу окружности ВС. Тогда
Если угол отклонения невелик, то можно считать, что сила F направлена по радиусу окружности ВС. Тогда Треугольники ОВС и BDE подобны, поэтому можно записать: ОС : СВ = BD : BE. Так как ОС = h, ВС = R, BD = Fтяж, a BE = F, то:
Треугольники ОВС и BDE подобны, поэтому можно записать: ОС : СВ = BD : BE. Так как ОС = h, ВС = R, BD = Fтяж, a BE = F, то: Приравнивая выражения (2) и (3), получаем выражение для скорости обращения конического маятника:
Приравнивая выражения (2) и (3), получаем выражение для скорости обращения конического маятника: Наконец, подставляя выражение (4) в выражение (1), получаем
Наконец, подставляя выражение (4) в выражение (1), получаем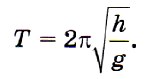 При малых отклонениях маятника h ≈ 1. Если длина нити l = 1 м, а отклонение маятника составляет R = 5 см, то по теореме Пифагора можно найти величину h:
При малых отклонениях маятника h ≈ 1. Если длина нити l = 1 м, а отклонение маятника составляет R = 5 см, то по теореме Пифагора можно найти величину h:![]()
Следовательно, для малых углов можно записать: Именно в таком виде записывается формула периода колебаний математического маятника.
Именно в таком виде записывается формула периода колебаний математического маятника.
Зависимость периода колебаний маятника от ускорения свободного падения позволяет опытным путём определить значение g. По изменению значения g на одной и той же географической широте можно судить о наличии месторождений полезных ископаемых. Подобные измерения позволили открыть Курскую магнитную аномалию.
Исследуя колебания маятника, Галилей установил, что время качаний маятников разной длины пропорционально квадратным корням из их длин. В 1638 г. он сформулировал этот закон в книге «Беседы и математические доказательства, касающиеся двух новых отраслей…».
Вы смотрели Конспект по физике для 9 класса «Период колебаний математического маятника».
Вернуться к Списку конспектов по физике (Оглавление).