Конспект по физике для 9 класса «Гармонические колебания. Затухающие колебания». ВЫ УЗНАЕТЕ: Какие колебания называются гармоническими. Что представляет собой график гармонических колебаний. Какие превращения энергии происходят при колебаниях маятника. Что такое затухающие колебания.
Конспекты по физике Учебник физики Тесты по физике
Гармонические колебания.
Затухающие колебания
Среди различных колебательных процессов выделяется особый вид колебаний, которые называют гармоническими. Этот вид колебаний является основным для дальнейшего изучения более сложных колебательных систем.
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Вы уже знаете, что если пренебречь силой трения, то на груз пружинного маятника будет действовать сила упругости пружины. Она согласно закону Гука зависит от коэффициента жёсткости пружины k, пропорциональна смещению (т. е. отклонению груза от положения равновесия) и направлена к положению равновесия: Fynp = –kx. Знак «минус» здесь означает, что направление силы упругости противоположно направлению смещения груза.
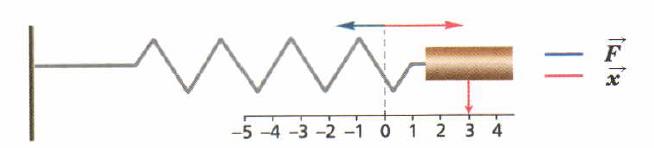
Рассмотрим математический (нитяной) маятник. Колебания математического маятника обусловлены тем, что равнодействующая силы тяжести и силы упругости F = Fтяж + Fупр, действующая на груз, отлична от нуля. Обозначим через х величину смещения груза. Хотя перемещение происходит по дуге, но при малых углах отклонения можно не учитывать различия между длиной дуги и величиной смещения. Рассмотрим два подобных треугольника ОВС и DBE. Отношение соответствующих катетов равно отношению гипотенуз, т. е.
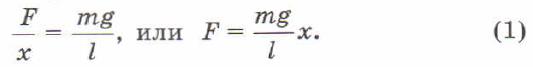
Величина mg/l во время колебаний не меняется. Обозначим:

Тогда выражение для модуля возвращающей силы можно записать следующим образом: F = kx. При этом её направление противоположно направлению смещения груза. Получается, что как для пружинного маятника, так и для математического маятника возвращающая сила направлена в сторону, противоположную смещению, и пропорциональна ему, т. е. F ∼ –х.
Колебания, которые происходят под действием силы, пропорциональной смещению колеблющегося тела из положения равновесия и направленной противоположно этому смещению, называют гармоническими.
Конечно, гармонические колебания рассматриваются как модель, так как в реальности всегда присутствуют силы трения и сопротивления среды.
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИИ
Используем в качестве груза маятника сосуд с красящей жидкостью и под ним расположим бумажную ленту, движущуюся с постоянной скоростью. Получившуюся кривую называют осциллограммой (от лат. oscillum — колебание и греч. gamma — запись). А рассмотренный прибор является простейшим осциллографом — прибором для записи колебаний.
Бумажная лента равномерно движется в течение некоторого промежутка времени, поэтому можно связать ось времени с направлением её движения. Проведя ось времени через точки, соответствующие прохождению грузом положения равновесия, мы получим график зависимости координаты от времени в гармонических колебаниях. С помощью графика колебаний можно определить положение тела в любой момент времени.
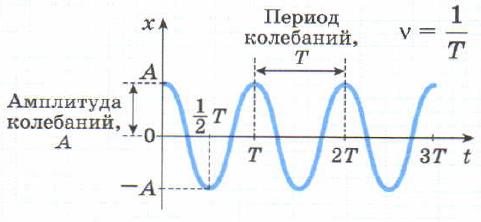
Кривые, подобные изображённой на рисунке, называются синусоидами. Подробнее вы узнаете об этом в старших классах.
СОХРАНЕНИЕ ЭНЕРГИИ ПРИ КОЛЕБАНИЯХ
Когда математический маятник покоится в положении равновесия, его кинетическая энергия равна нулю. Примем за нулевой уровень отсчёта потенциальной энергии маятника его положение равновесия. Поэтому здесь равна нулю и его полная механическая энергия.
Когда маятник отклоняют на высоту h над нижним положением, его потенциальная энергия максимальна и равна EП = mgh.
Когда маятник отпускают, потенциальная энергия переходит в энергию кинетическую, причём в нижней точке траектории, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке: 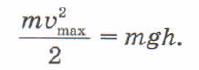
При этом полная механическая энергия колебательной системы остаётся постоянной.
Казалось бы, такие колебания не должны затухать. Однако наличие силы трения и силы сопротивления среды приводит к тому, что происходит потеря механической энергии за счёт её превращения во внутреннюю энергию.
Незатухающие свободные колебания, которые происходили бы в колебательной системе в отсутствие трения, называются собственными колебаниями системы.
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
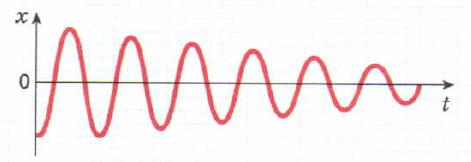
Под влиянием силы трения происходит уменьшение амплитуды колебаний и через некоторое время колебания прекращаются. Такие колебания с уменьшающейся амплитудой называют затухающими. Причём, чем больше силы сопротивления движению, тем быстрее прекращаются колебания.
Если механическая энергия колебательной системы достаточно велика, а трение в ней мало, то колебания с небольшой амплитудой можно считать приблизительно гармоническими. Полностью пренебречь затуханием можно лишь рассматривая небольшое число колебательных движений.
Вы смотрели Конспект по физике для 9 класса «Гармонические колебания. Затухающие колебания».
Вернуться к Списку конспектов по физике (Оглавление).