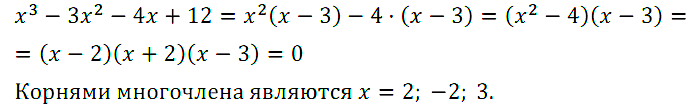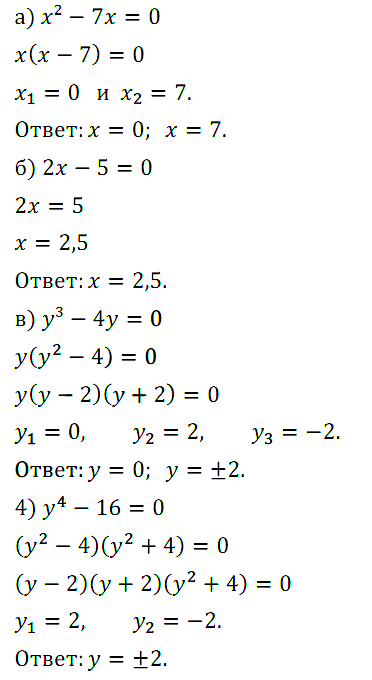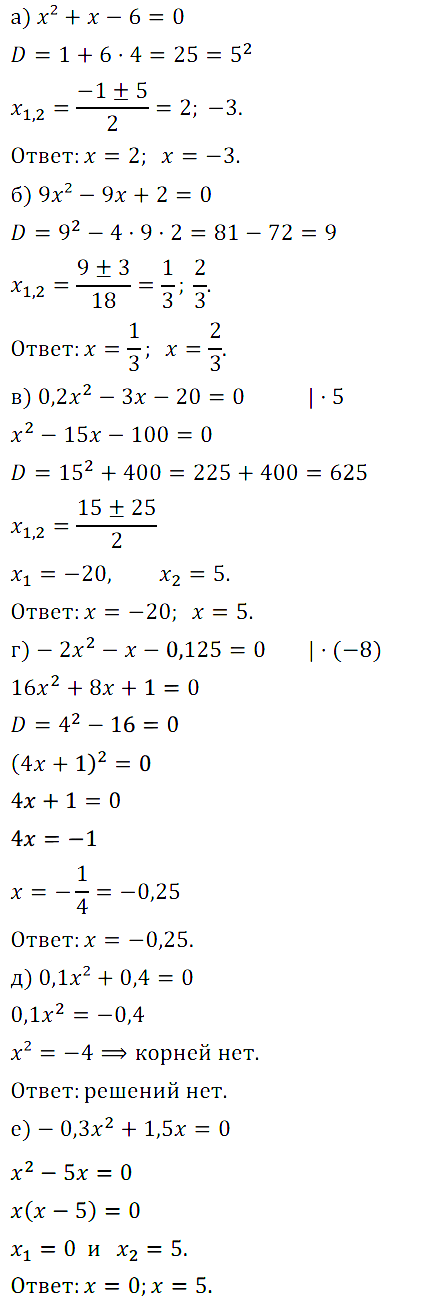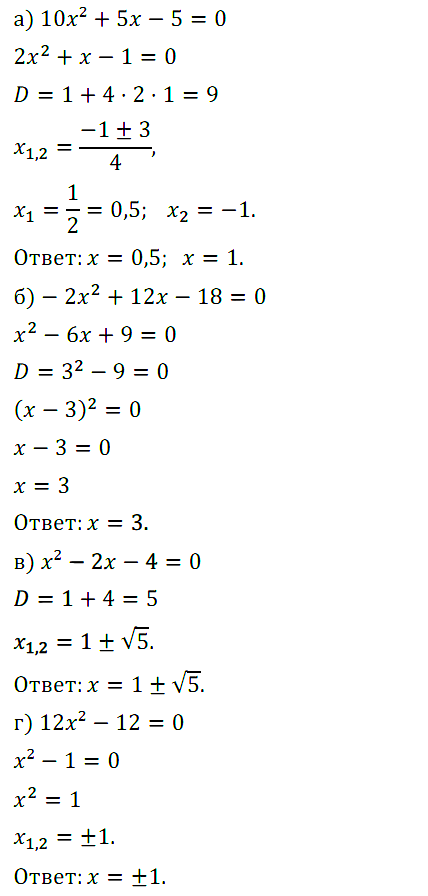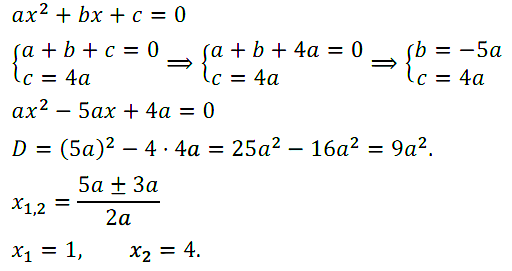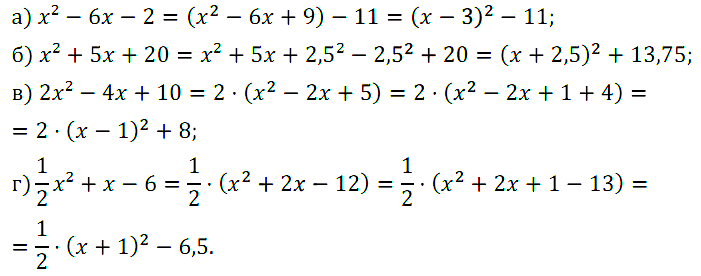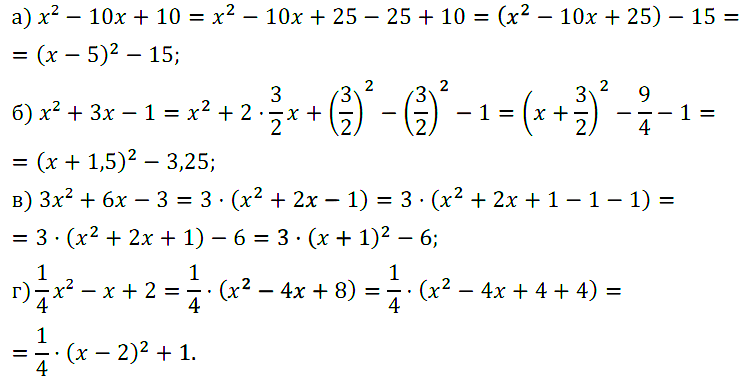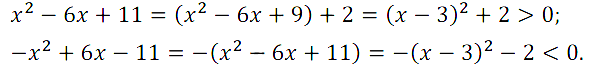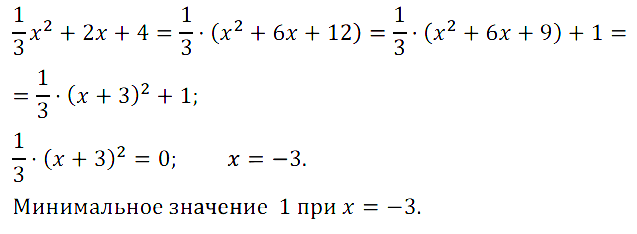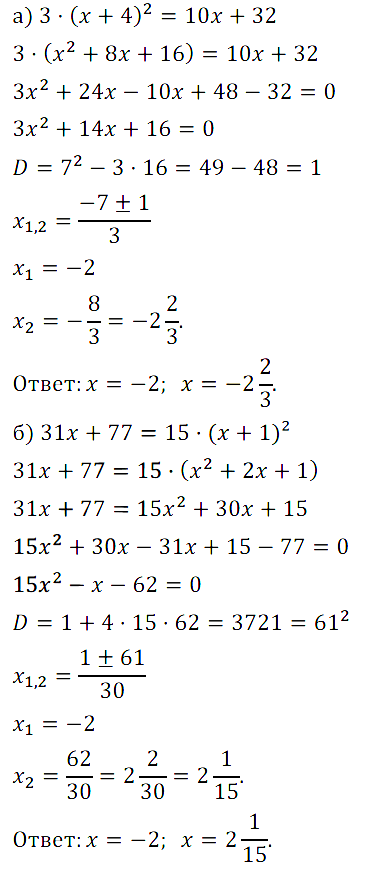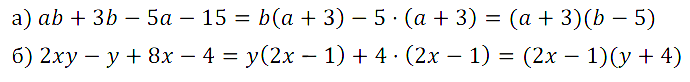Алгебра 9 класс УМК Макарычев, Миндюк, Нешков, Суворова. Упражнения №№ 55 — 75 из учебника с ответами и решениями. § 2. КВАДРАТНЫЙ ТРЁХЧЛЕН. 3. Квадратный трёхчлен и его корни. Алгебра 9 Макарычев Упражнения 55-75 + ОТВЕТЫ.
О Г Л А В Л Е Н И Е Вернуться к списку тем учебника
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Алгебра 9 класс (Макарычев)
§ 2. Упражнения №№ 55 — 75
Задание № 55. Какие из чисел –2, –1, 0, 2, 3 являются корнями многочлена х3 – 3x2 – 4х + 12?
Задание № 56. Найдите корни многочлена:
а) x2 – 7х; б) 2х – 5; в) y3 – 4у; г) у4 – 16.
Задание № 57. Имеет ли корни многочлен:
а) x2 + 1; б) х3 – 27; в) –2у6 – 1; г) у4 + 3y2 + 7?
Задание № 58. Какие из чисел 1, 2, 3 – √2, –7 + √2 являются корнями квадратного трёхчлена x2 – 6х + 7?
Задание № 59. Найдите корни квадратного трёхчлена:
а) x2 + х – 6; г) –2x2 – х – 0,125;
б) 9x2 – 9х + 2; д) 0,1x2 + 0,4;
в) 0,2x2 + 3х – 20; е) –0,3x2 + 1,5х.
Задание № 60. Найдите корни квадратного трёхчлена:
а) 10x2 + 5х – 5; в) x2 – 2х – 4;
б) –2x2 + 12х – 18; г) 12x2 – 12.
Задание № 61. Имеет ли квадратный трёхчлен корни и если имеет, то сколько:
а) 5x2 – 8х + 3; в) –7x2 + 6х – 2;
б) 9x2 + 6х + 1; г) –x2 + 5х – 3?
Задание № 62. Имеет ли квадратный трёхчлен корни и если имеет, то сколько:
а) –4x2 – 4х + 3; в) 9x2 – 12х + 4;
б) 4x2 – 4х + 3; г) 9x2 – 12х – 4?
Задание № 63. Сумма коэффициентов квадратного трёхчлена равна нулю, а его свободный член в 4 раза больше старшего коэффициента. Найдите корни этого трёхчлена.
Задание № 64. Выделите квадрат двучлена из квадратного трёхчлена:
а) x2 – 6х – 2; в) 2x2 – 4х + 10;
б) x2 + 5х + 20; г) x2/2 + х – 6.
Задание № 65. Выделите квадрат двучлена из квадратного трёхчлена:
а) x2 – 10х + 10; в) 3x2 + 6х – 3;
б) x2 + 3х – 1; г) x2/4 – х + 2.
Задание № 66. (Для работы в парах.) Докажите, что при любом значении х квадратный трёхчлен:
а) x2 – 6х + 10 принимает положительное значение;
б) 5x2 – 10х + 5 принимает неотрицательное значение;
в) –x2 + 20х – 100 принимает неположительное значение;
г) –2x2 + 16х – 33 принимает отрицательное значение;
д) x2 – 0,32х + 0,0256 принимает неотрицательное значение;
е) 4x2 + 0,8х + 2 принимает положительное значение.
1) Обсудите, какие преобразования трёхчленов надо выполнить для доказательства высказанных утверждений.
2) Распределите, кто выполняет задания а), в) и д), а кто – задания б), г) и е), и выполните их.
3) Проверьте друг у друга правильность проведённых доказательств и исправьте ошибки, если они допущены.
Задание № 67. Даны квадратные трёхчлены x2 – 6x + 11 и –x2 + 6x – 11.
Докажите, что первый из них не принимает отрицательных значений, а второй – положительных.
Задание № 68. При каком значении х трёхчлен 2x2 – 4х + 6 принимает наименьшее значение? Найдите это значение.
Задание № 69. Дан квадратный трёхчлен x2/3 + 2х + 4. Выясните, при каком значении х он принимает наименьшее значение и чему равно это значение трёхчлена.
Задание № 70. (Задача–исследование.) Выясните, какой из прямоугольных треугольников с суммой катетов, равной 6 см, имеет наибольшую площадь. Вычислите эту площадь.
1) Обозначьте длину одного из катетов через х см и составьте выражение для вычисления площади треугольника.
2) Исследуйте, при каких значениях переменной составленное выражение принимает наибольшее значение.
3) Вычислите, чему равно значение площади треугольника при указанных значениях переменной.
Задание № 71. С башни выпустили вверх стрелу из лука. Если начальная скорость стрелы равна 50 м/с, высота башни 20 м и t (с) – время полёта стрелы, то расстояние h (м) стрелы от поверхности земли в момент времени t (с) можно найти по формуле h = –5t2 + 50t + 20 (приближённое значение ускорения свободного падения считается равным 10 м/с2). Какой наибольшей высоты достигнет стрела?
Задание № 72. .
Задание № 73. .
Задание № 74. .
Задание № 75. .
Вы смотрели: Алгебра 9 класс УМК Макарычев. Упражнения из учебника с ответами и решениями. Глава 1. КВАДРАТИЧНАЯ ФУНКЦИЯ. § 2. КВАДРАТНЫЙ ТРЁХЧЛЕН. 3. Квадратный трёхчлен и его корни. Алгебра 9 Макарычев Упражнения 55-75 + ОТВЕТЫ.