С О Д Е Р Ж А Н И Е Вернуться к списку тем учебника
Алгебра 9 класс. УМК Макарычев и др. Онлайн-учебник 2017. Глава 1. КВАДРАТИЧНАЯ ФУНКЦИЯ. § 1. ФУНКЦИИ И ИХ СВОЙСТВА. (1. Функция. Область определения и область значений функции. 2. Свойства функций) Электронная версия.
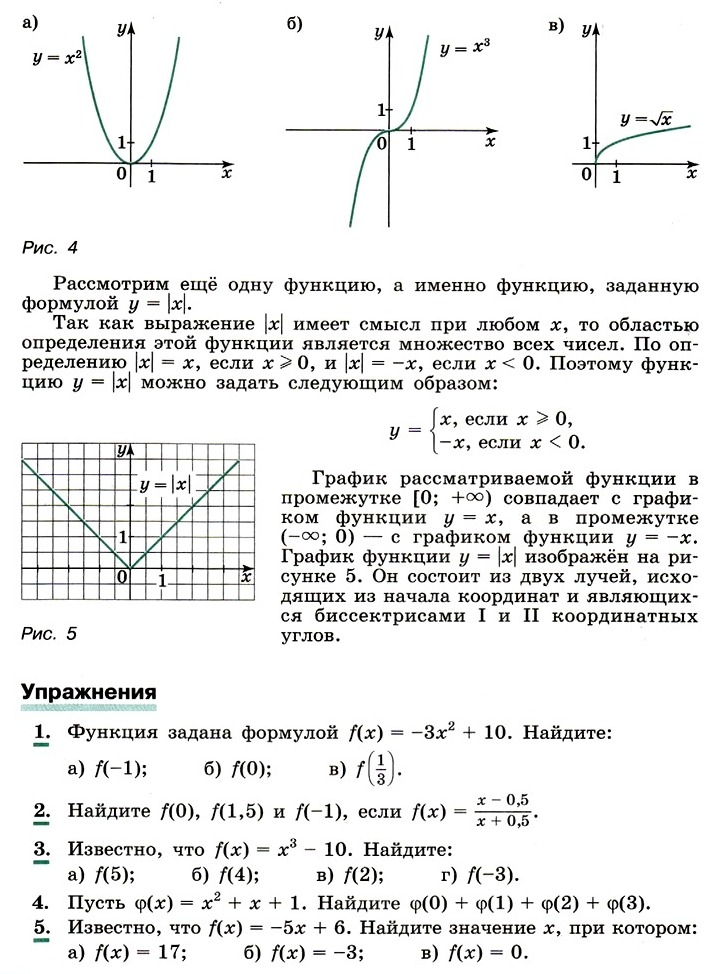
В курсе алгебры 7 и 8 классов вы уже многое узнали о функциях. В этой главе сведения о функциях будут расширены. Здесь вводятся новые понятия — область значений, возрастание и убывание функции. Основное внимание уделяется квадратичной функции. Вы узнаете о свойстве параболоида — тела, которое получается при вращении параболы вокруг её оси. Вас, вероятно, заинтересует легенда о том, как использовал это свойство древнегреческий учёный Архимед (III в. до н. э.) при защите Сиракуз. В заключительной части главы вы познакомитесь со свойствами степенной функции у = хn, где n — натуральное число, узнаете, что график этой функции при чётном п сходен с графиком функции у = х2, а при нечётном — с графиком функции у = х3. При получении свойств квадратичной и степенной функций рекомендуем использовать компьютер.
§ 1. Функции и их свойства
1. Функция. Область определения и область значений функции.
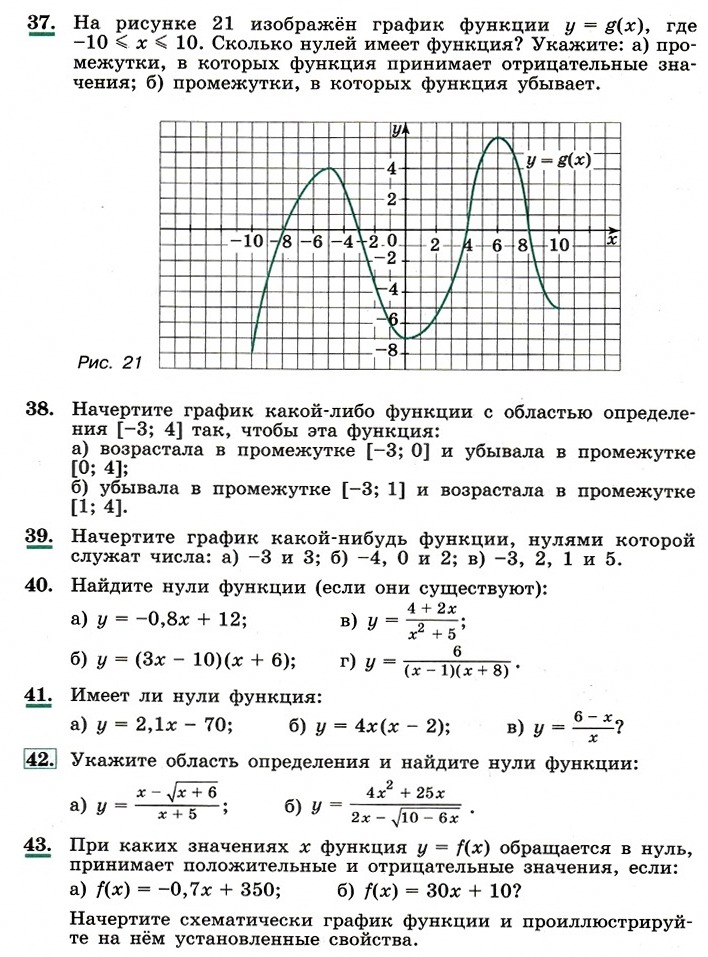
2. Свойства функций
С О Д Е Р Ж А Н И Е Вернуться к списку тем учебника
Алгебра 9 Макарычев. Онлайн-учебник 2017. Глава 1. КВАДРАТИЧНАЯ ФУНКЦИЯ. § 1. ФУНКЦИИ И ИХ СВОЙСТВА. (1. Функция. Область определения и область значений функции. 2. Свойства функций) Электронная версия.