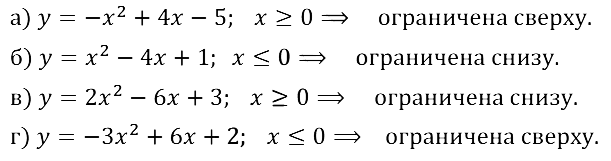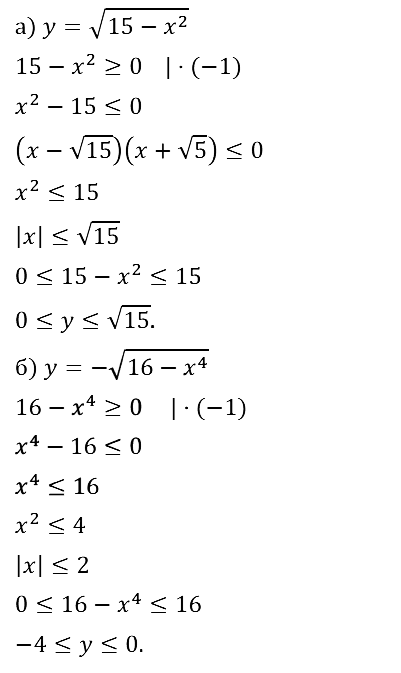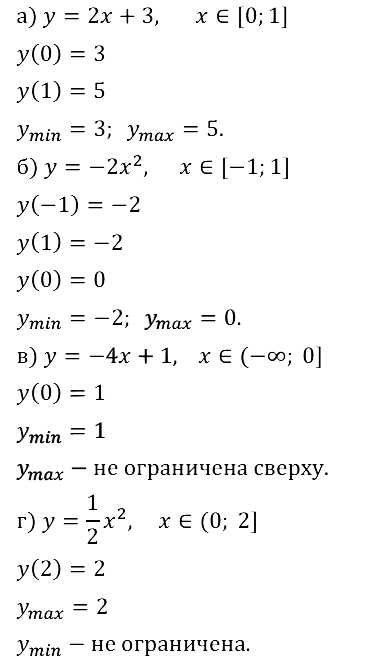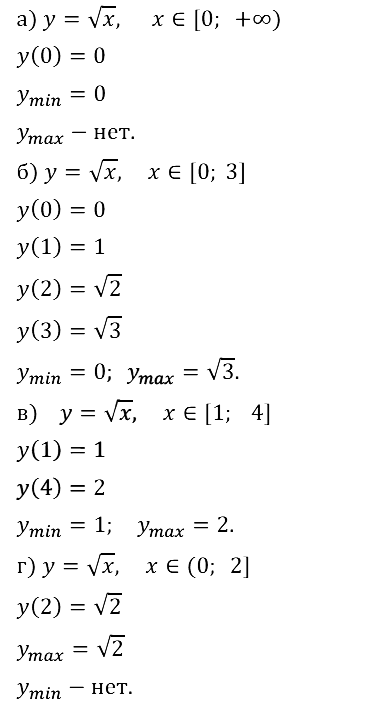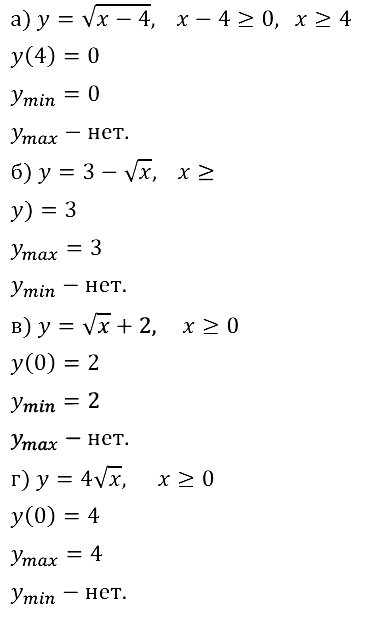Частная школа. 9 класс

Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ОТВЕТЫ на упражнения 10.1 — 10.28. § 10. Свойства функций. ГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИ.

ОГЛАВЛЕНИЕ Вернуться к списку тем учебника

 

Алгебра 9 класс (Мордкович)
Упражнения №№ 10.1 — 10.28

Нажмите на спойлер, чтобы посмотреть ответ на задание.

ГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИ

§ 10. Свойства функций

Используя свойства числовых неравенств, докажите, что заданная функция возрастает:

Задание № 10.1. а) у = 5х;   б) у = 2х + 3;   в) у = 2х – 3;   г) y = x/2 + 4.

Задание № 10.2. а) у = х³;   б) у = 2х³;   в) у = х³ + 1;   г) y = x³/2.

Задание № 10.3. а) у = x², х ≥ 0; б) у = –1/x, x < 0; в) у = –1/x, х > 0; г) у = –Зx², х ≤ 0.

Задание № 10.4. а) у = –5х;   б) у = 5 – 2х;   в) у = –7х + 1;   г) y = 4 – x/3.

Задание № 10.5. а) у = –х³;   б) у = –3х³;   в) y = –x³/5;   г) y = –x³ + 7.

Задание № 10.6.

Для данной функции ответьте на вопрос, является ли она ограниченной снизу, ограниченной сверху, ограниченной:

Задание № 10.7. a) y = 7x+ 2;   б) у = –3x + 1, х < 0;   в) у = 4х + 1, х > 0;   г) у = –2х + 5, 0 ≤ х ≤ 5.

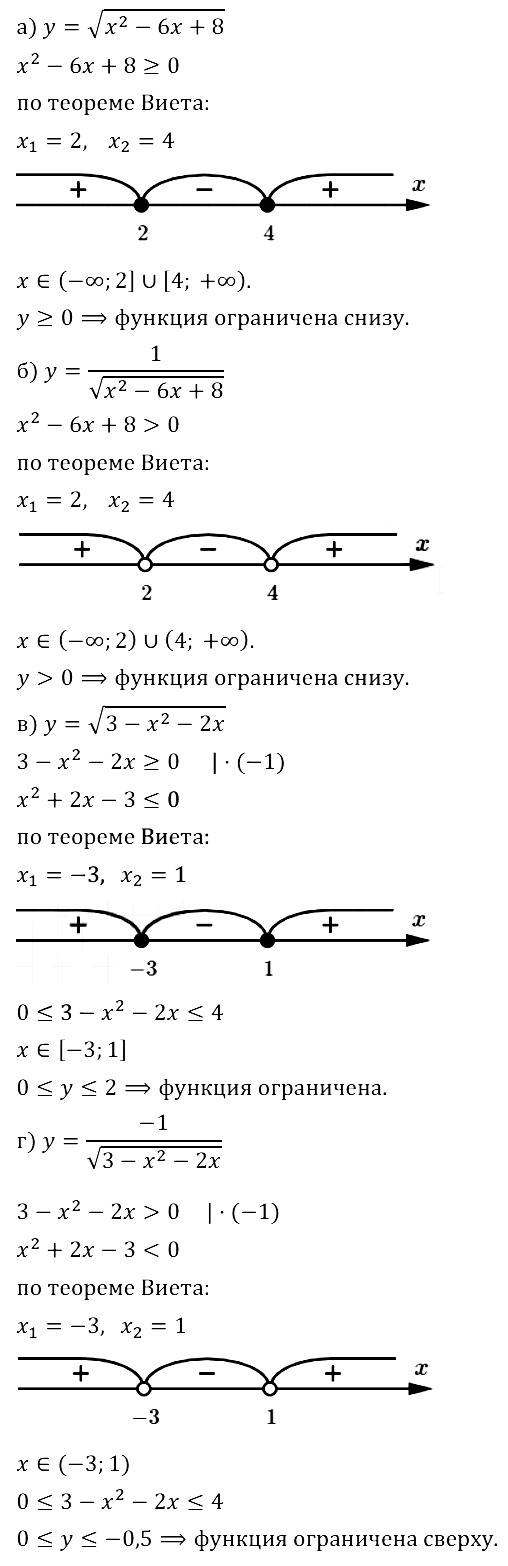
Задание № 10.8.

Задание № 10.9.

Задание № 10.10.

Задание № 10.11.

Задание № 10.12.

Задание № 10.13.

Задание № 10.14.

Задание № 10.15.

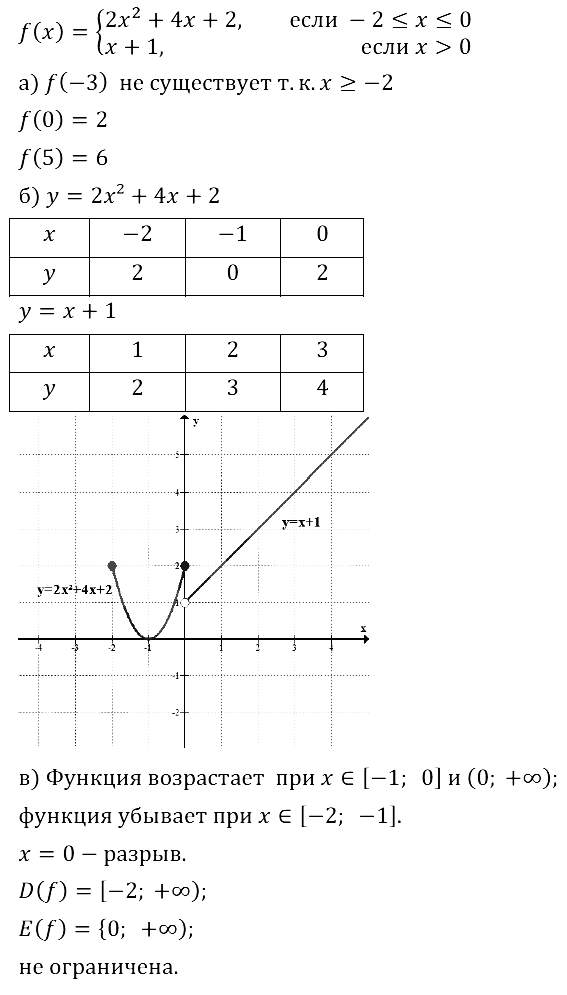
Задание № 10.16. Дана функция у = f(x), где f(x) =
{ 2x² + 4х + 2, если –2 ≤ х ≤ 0;
{ x + 1, если x > 0.
а) Найдите: f(–3); f(0); f(5);
б) постройте график функции у = f(x);
в) перечислите свойства функции.

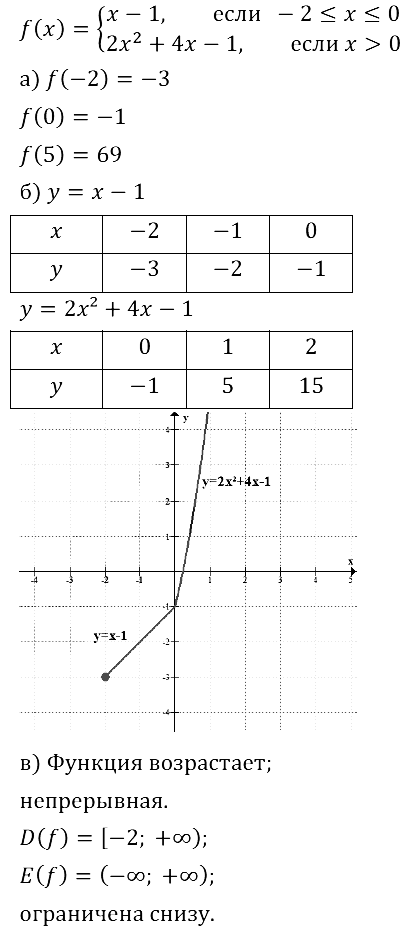
Задание № 10.17. Дана функция у = f(x), где f(x) =
{ x — 1, если —2 ≤ x ≤ 0;
{ 2x² + 4х –1, если х > 0.
а) Найдите: f(–2); f(0); f(5);
б) постройте график функции у = f(x);
в) перечислите свойства функции.

Докажите, что функция возрастает:

Задание № 10.18. а) у = х³ + 3x;   б) у = x⁴ + 3x, х ≥ 0;   в) у = 2x³ + x;   г) у = 2x⁴ + x, x ≥ 0.

Задание № 10.19.

Задание № 10.20. Докажите, что функция убывает:
а) у = –х³ – 2х;   б) у = х⁶ – 0,5х, х ≤ 0;   в) у = х⁴ – 5х, х ≤ 0;   г) у = –3х⁵ – х.

Найдите наименьшее и наибольшее значения функции:

Задание № 10.21.  а) у = x² + 4х – 3;   б) у = –4x² – 12x + 1;   в) y = 9x² + 6х – 5;   г) у = –x² + 8х – 12.

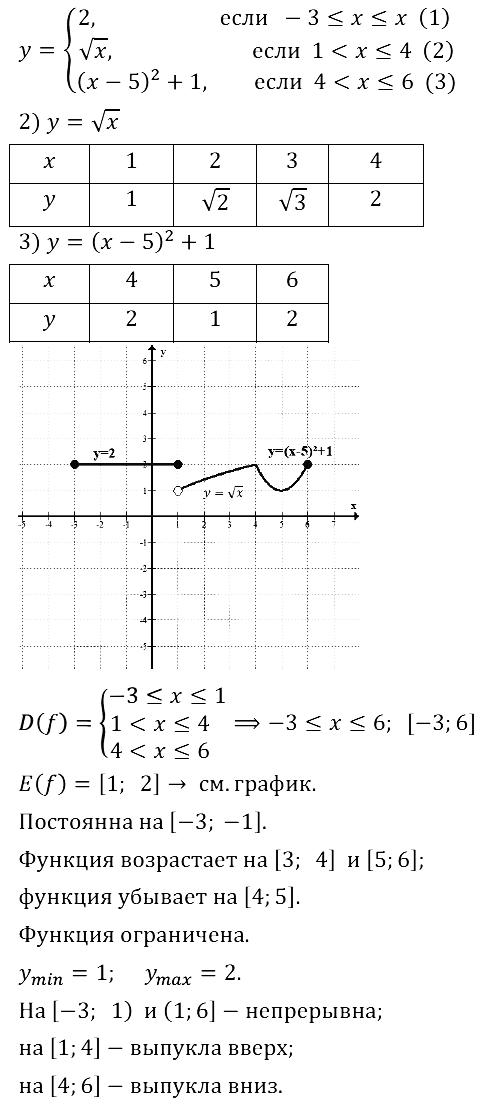
Задание № 10.22.

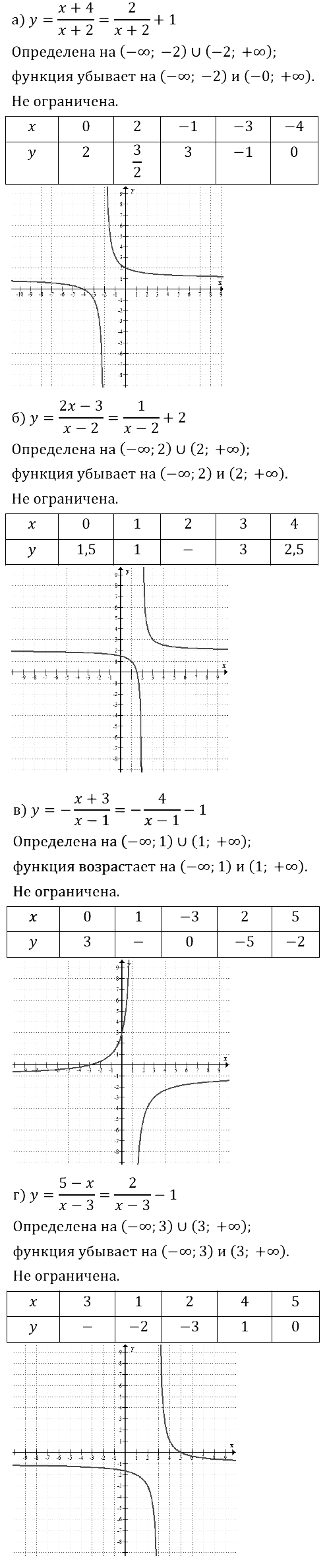
Задание № 10.23. Представьте данную функцию в виде у = f(x + l) + m, опишите её свойства и постройте график: а) у = (x + 4)/(x + 2); …

Задание № 10.24. Представьте данную функцию в виде у = f(x + l) + m, опишите её свойства и постройте график: a) y = (x – 5)/(4 – x), x > 4; …

Задание № 10.25.

Задание № 10.26.

Задание № 10.27.

Задание № 10.28. Найдя промежутки монотонности функции у = f(x), сравните f(а) и f(b), если:
а) f(x) = 3,7x² х – 7,4x – 9, а = 2,9, b = 3,1;
б) f(x) = –4,1x² – 16,4x + 3, а = –1,8, b = –1,3;
в) f(x) = 1,9x² + 5,7x + 4, а = –5,2, b = –2,2;
г) f(x) = –3,3x² + 3,3x, а = 0,55, b = 0,53.

 

 

---

Вы смотрели: ГДЗ Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИ. § 10. Свойства функций. ОТВЕТЫ на задачи 10.1 — 10.28.