Контрольная работа по алгебре в 9 класс «Квадратичная функция» (варианты 3-4) с ответами и решениями для УМК Дорофеев. Цитаты из пособия авторов — Кузнецова, Минаева, Рослова, Суворова — использованы в учебных целях для семейного и домашнего обучения. Алгебра Дорофеев Контрольная 2 В34 + Ответы.
Вернуться в ОГЛАВЛЕНИЕ Контрольная 2 Варианты 1-2
Алгебра (УМК Дорофеев)
Контрольная работа № 2
К-2 Вариант 3 (задания)
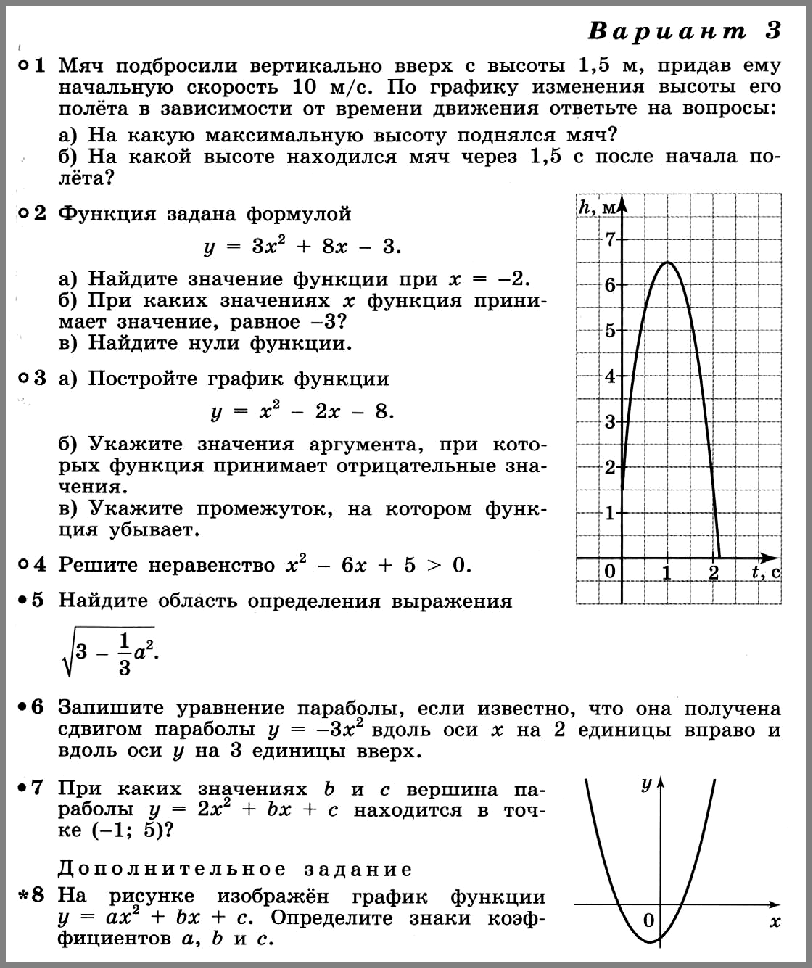
- Мяч подбросили вертикально вверх с высоты 1,5 м, придав ему начальную скорость 10 м/с. По графику изменения высоты его полёта в зависимости от времени движения ответьте на вопросы:
а) На какую максимальную высоту поднялся мяч?
б) На какой высоте находился мяч через 1,5 с после начала полёта? - Функция задана формулой у = 3x2 + 8x – 3.
а) Найдите значение функции при х = –2.
б) При каких значениях х функция принимает значение, равное –3?
в) Найдите нули функции. - а) Постройте график функции у – х2 – 2х – 8.
б) Укажите значения аргумента, при которых функция принимает отрицательные значения.
в) Укажите промежуток, на котором функция убывает. - Решите неравенство х2 – 6х + 5 > 0.
- Найдите область определения выражения √[3 – 1/3 • a2].
- Запишите уравнение параболы, если известно, что она получена сдвигом параболы у = –3x2 вдоль оси х на 2 единицы вправо и вдоль оси у на 3 единицы вверх.
- При каких значениях b и с вершина параболы у = 2х2 + bx + с находится в точке (–1; 5)?
Дополнительное задание.
8. * На рисунке изображён график функции у = ах2 + bx + с. Определите знаки коэффициентов а, b и с.
К-2 Вариант 4 (задания)
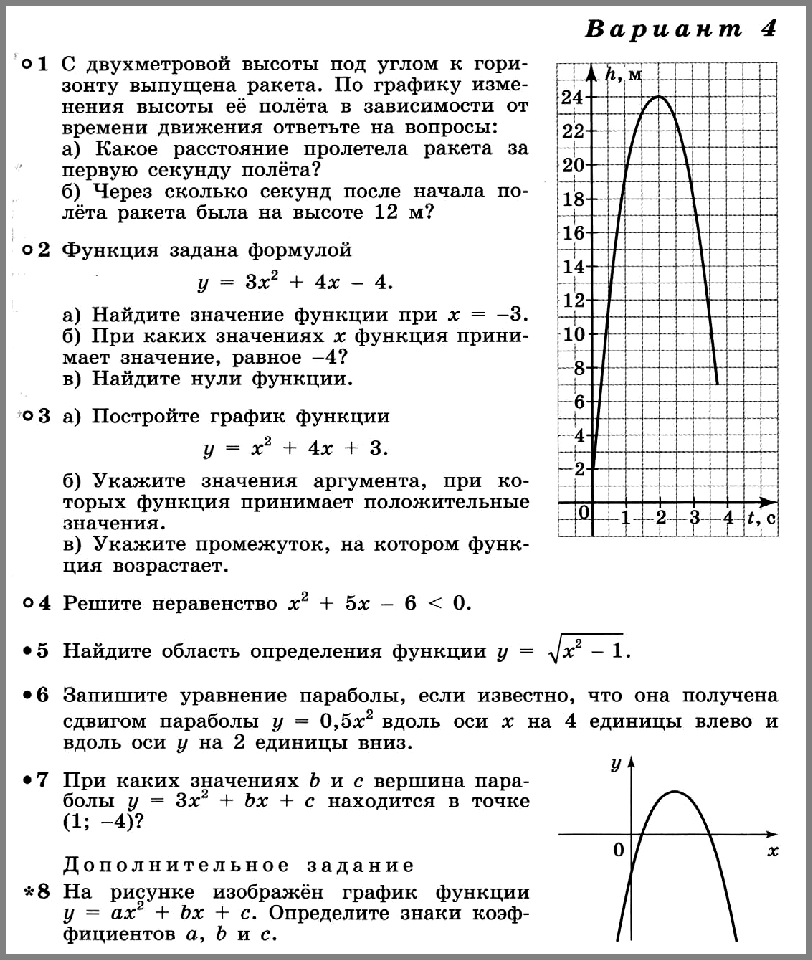
- С двухметровой высоты под углом к горизонту выпущена ракета. По графику изменения высоты её полёта в зависимости от времени движения ответьте на вопросы:
а) Какое расстояние пролетела ракета за первую секунду полёта?
б) Через сколько секунд после начала полёта ракета была на высоте 12 м? - Функция задана формулой у = 3x2 + 4х – 4.
а) Найдите значение функции при х = –3.
б) При каких значениях х функция принимает значение, равное –4?
в) Найдите нули функции. - а) Постройте график функции у = х2 + 4х + 3.
б) Укажите значения аргумента, при которых функция принимает положительные значения.
в) Укажите промежуток, на котором функция возрастает. - Решите неравенство х2 + 5х – 6 < 0.
- Найдите область определения функции у = √[х2 – 1].
- Запишите уравнение параболы, если известно, что она получена сдвигом параболы у = 0,5х2 вдоль оси х на 4 единицы влево и вдоль оси у на 2 единицы вниз.
- При каких значениях b и с вершина параболы у = 3x2 + bx + с находится в точке (1; –4)?
Дополнительное задание.
8. * На рисунке изображён график функции у = ах2 + bx + с. Определите знаки коэффициентов а, b и с.
ОТВЕТЫ на вариант 3

Вернуться в ОГЛАВЛЕНИЕ Контрольная 2 Варианты 1-2
Алгебра Дорофеев Контрольная 2 в34
ОТВЕТЫ на вариант 4

Вы смотрели: Контрольная работа по алгебре в 9 класс «Неравенства» с ответами и решениями для УМК Дорофеев. Цитаты из пособия использованы в учебных целях для семейного и домашнего обучения. Алгебра Дорофеев Контрольная 2 В34 + Ответы.
Вернуться в ОГЛАВЛЕНИЕ Контрольная 2 Варианты 1-2