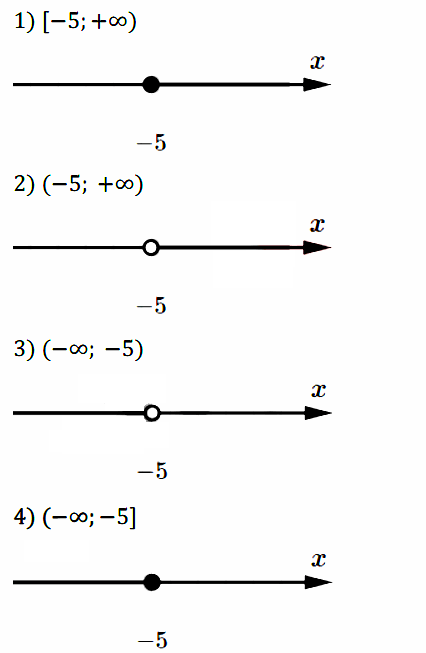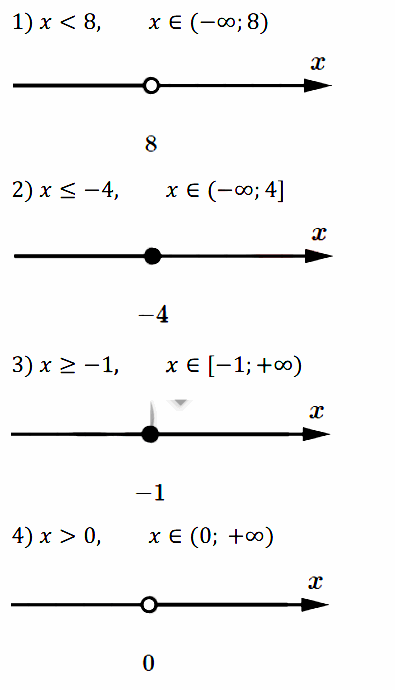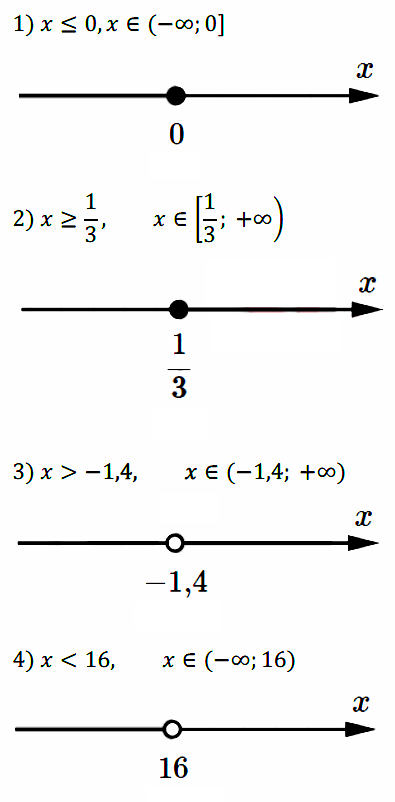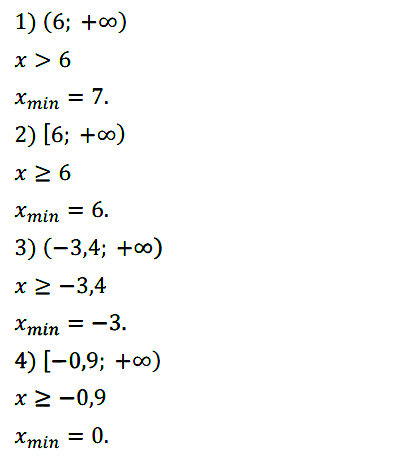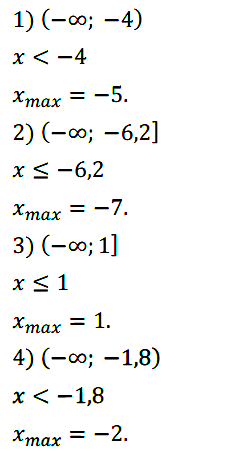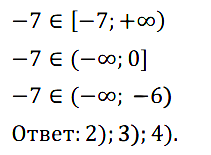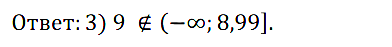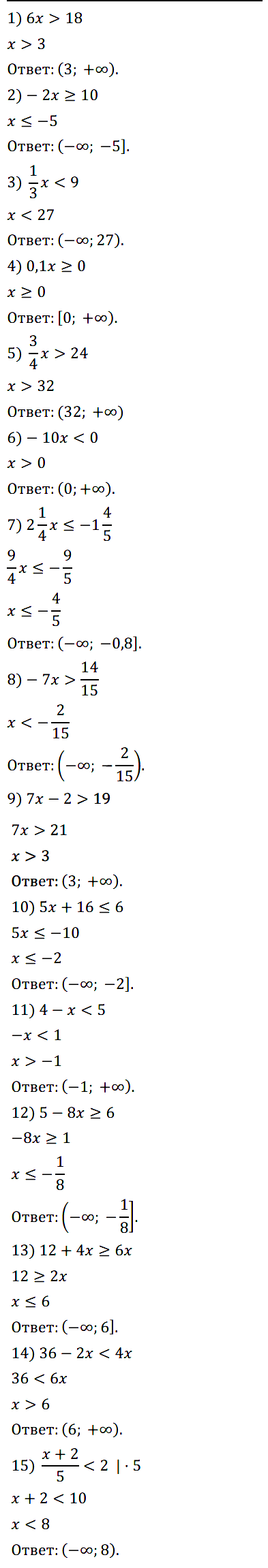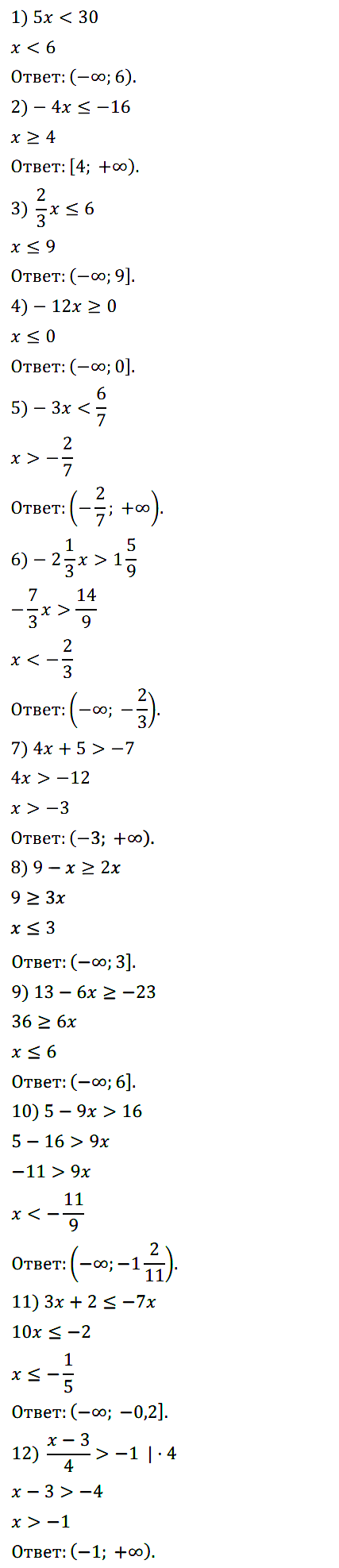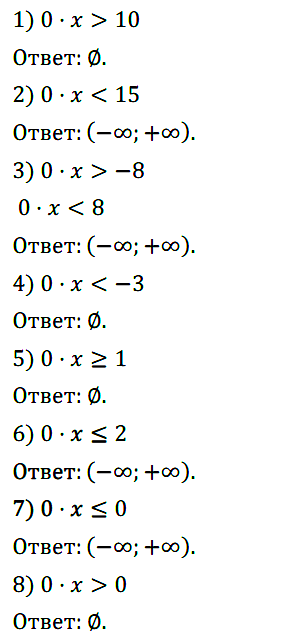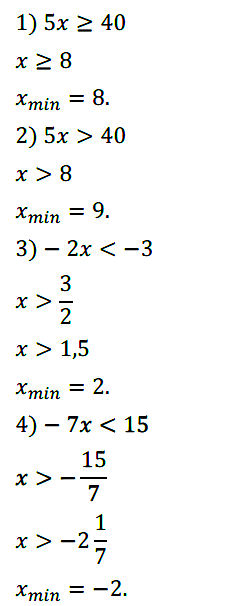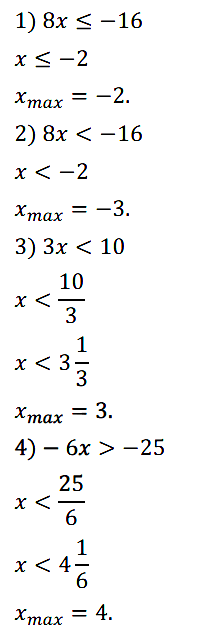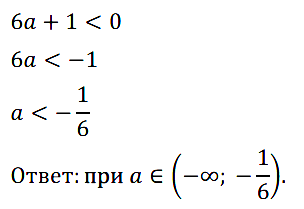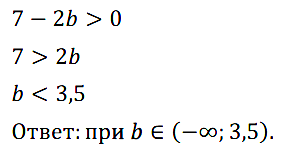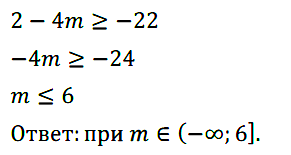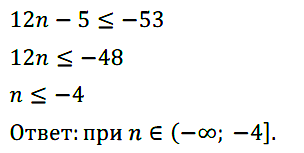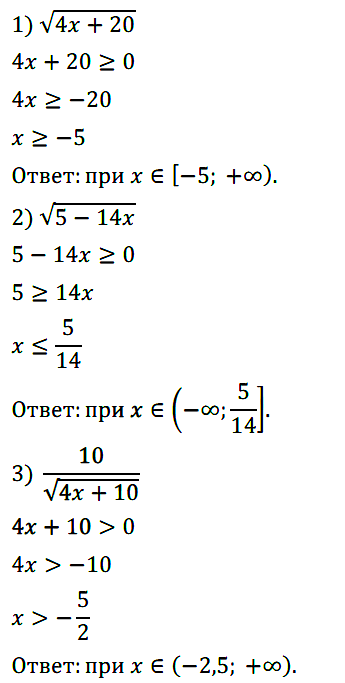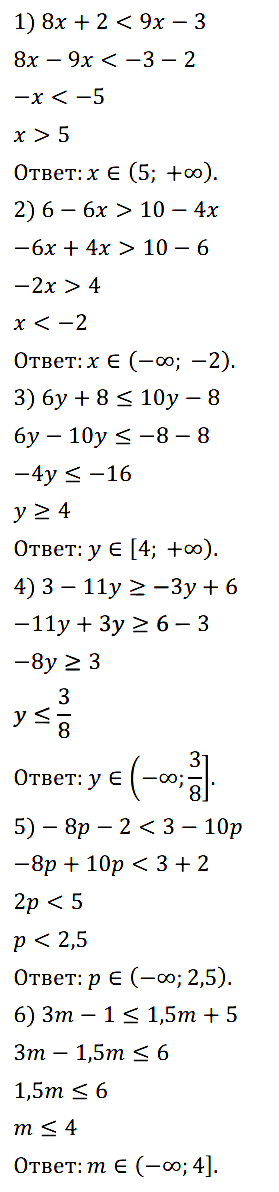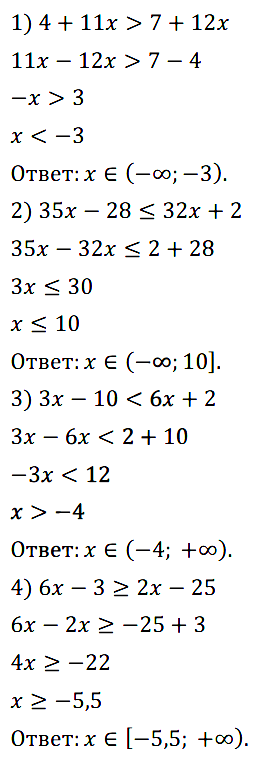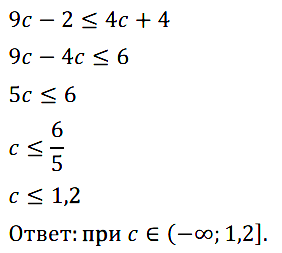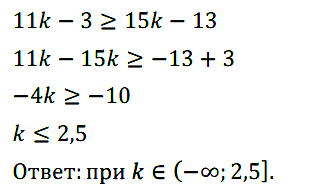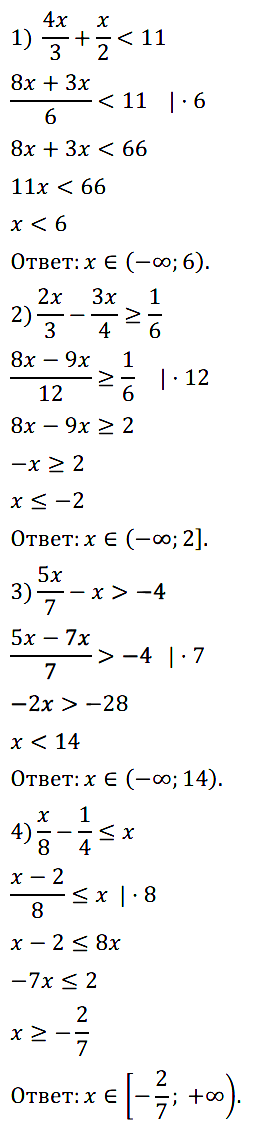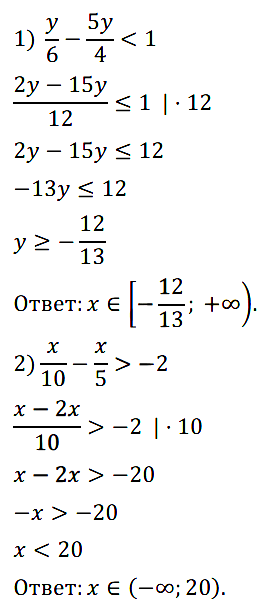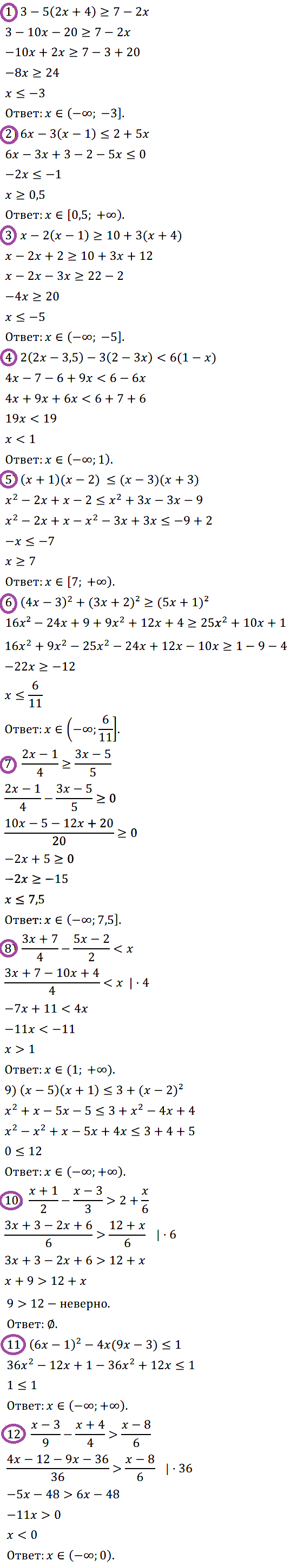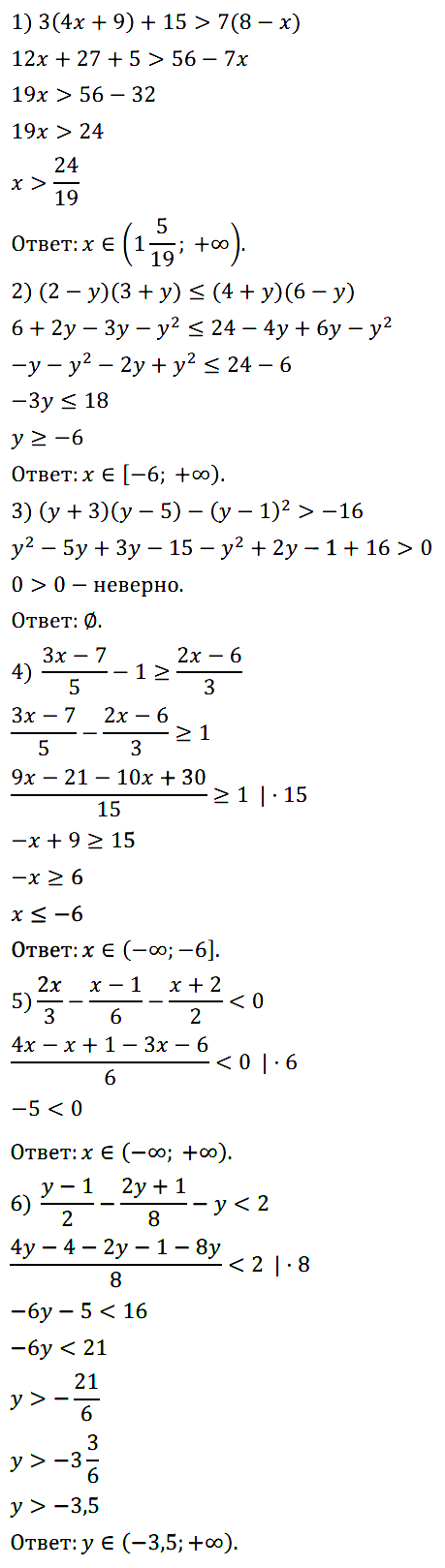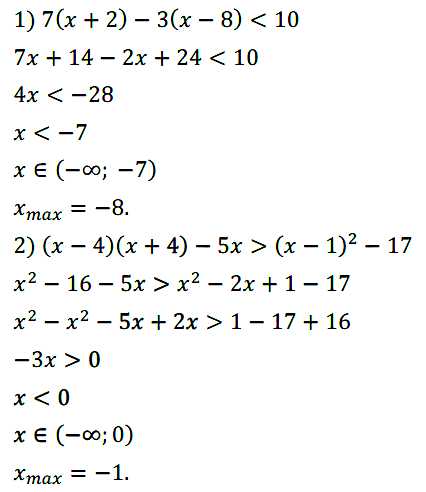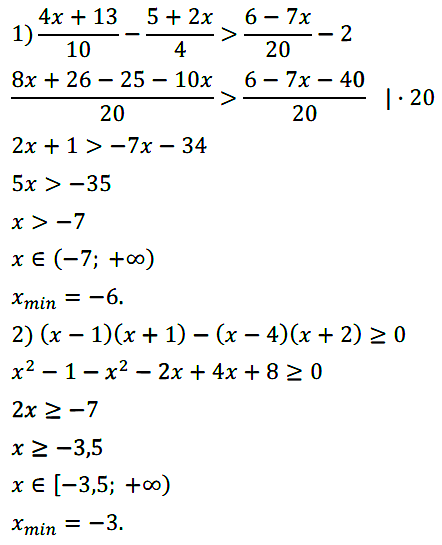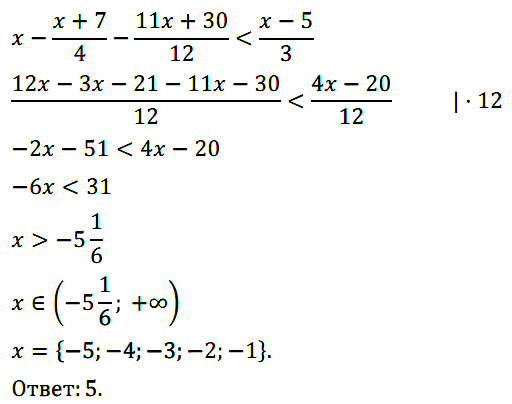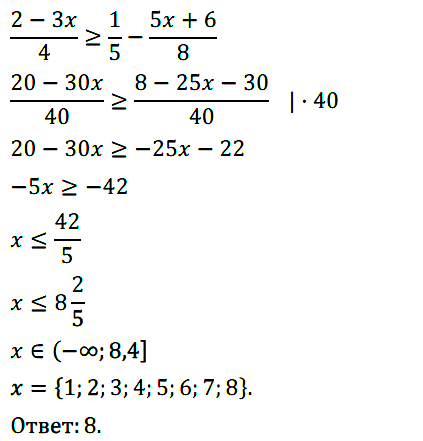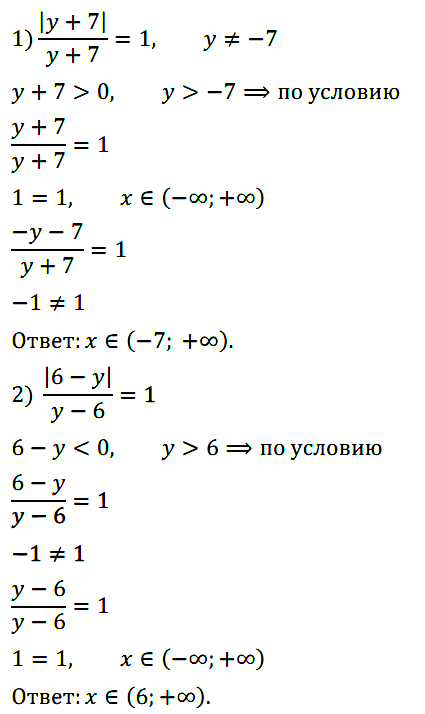ОГЛАВЛЕНИЕ Вернуться к списку тем учебника
Алгебра 9 класс УМК Мерзляк. Упражнения №№ 110 — 141 из учебника с ответами и решениями. Глава 1. НЕРАВЕНСТВА. § 5. Решение линейных неравенств с одной переменной. Числовые промежутки. Алгебра 9 Мерзляк Упражнения 110-141 + ОТВЕТЫ.
Алгебра 9 класс (Мерзляк)
Упражнения №№ 110 — 141
Нажмите на спойлер, чтобы посмотреть ответ на задание.
§ 5. Решение линейных неравенств с одной переменной.
Числовые промежутки
Задание № 110. Изобразите на координатной прямой промежуток:
1) [–5; +∞); 2) (–5; +∞); 3) (–∞; –5); 4) (–∞; –5].
Задание № 111. Изобразите на координатной прямой и запишите промежуток, который задаётся неравенством:
1) x < 8; 2) х ≤ –4; 3) х ≥ –1; 4) x > 0.
Задание № 112. Изобразите на координатной прямой и запишите промежуток, который задаётся неравенством:
1) x ≤ 0; 2) x ≥ 1/3; 3) x > –1,4; 4) х < 16.
Задание № 113. Укажите наименьшее целое число, принадлежащее промежутку:
1) (6; –∞); 2) [6; –∞); 3) (–3,4; +∞); 4) [–0,9; +∞).
Задание № 114. Укажите наибольшее целое число, принадлежащее промежутку:
1) (–∞; –4); 2) (–∞; –6,2]; 3) (–∞; 1]; 4) (–∞; –1,8).
Задание № 115. Каким из данных промежутков принадлежит число –7:
1) (–∞; –7); 2) [–7; +∞); 3) (–∞; 0]; 4) (–∞; –6) ?
Задание № 116. Какому из данных промежутков не принадлежит число 9:
1) (8,99; –∞); 2) (–∞; 10); 3) (–∞; 8,99]; 4) [9; +∞)?
Задание № 117.
Задание № 118. .
Задание № 119. Решите неравенство:
1) 0х > 10; 3) 0x > –8; 5) 0х ≥ 1; 7) 0х ≤ 0;
2) 0x < 15; 4) 0x < –3; 6) 0х ≤ 2; 8) 0х > 0.
Задание № 120. Найдите наименьшее целое решение неравенства:
1) 5х ≥ 40; 2) 5x > 40; 3) –2x < –3; 4) –7x < 15.
Задание № 121. Найдите наибольшее целое решение неравенства:
1) 8x < –16; 2) 8х < –16; 3) 3x < 10; 4) –6х > –25.
Задание № 122. При каких значениях а выражение 6а + 1 принимает отрицательные значения?
Задание № 123. При каких значениях b выражение 7 – 2b принимает положительные значения?
Задание № 124. При каких значениях m значения выражения 2 – 4m не меньше –22?
Задание № 125. При каких значениях n значения выражения 12n – 5 не больше –53?
Задание № 126. При каких значениях х имеет смысл выражение:
1) √[4х + 20]; 2) √[5 – 14x]; 3) 10/√[4x + 10] ?
Задание № 127. .
Задание № 128. Решите неравенство:
1) 8x + 2 < 9x – 3; 2) 6 – 6x > 10 – 4x; 3) 6y + 8 ≤ 10y – 8;
4) 3 – 11y ≥ –3y + 6; 5) –8р – 2 < 3 – 10р; 6) 3m – 1 ≤ 1,5m + 5.
Задание № 129. Решите неравенство:
1) 4 + 11x > 7 + 12x; 2) 35x – 28 ≤ 32x + 2;
3) 3x – 10 < 6x + 2; 4) 6x – 3 ≥ 2x – 25.
Задание № 130. При каких значениях с значения двучлена 9с – 2 не больше чем соответствующие значения двучлена 4с + 4?
Задание № 131. При каких значениях k значения двучлена 11k – 3 не меньше чем соответствующие значения двучлена 15k – 13 ?
Задание № 132. Решите неравенство:
1) 4x/3+ x/2 < 11; 2) 2x/3 – 3x/4 ≥ 1/6;
3) 5x/7 – x > –4; 4) x/8 – 1/4 ≤ x.
Задание № 133. Решите неравенство: 1) y/6 – 5y/4 < 1; 2) x/10 – x/5 > –2.
Задание № 134. .
Задание № 135. .
Задание № 136. .
Задание № 137. .
Задание № 138. .
Задание № 139. .
Задание № 140. .
Задание № 141. .
Вы смотрели: Алгебра 9 класс УМК Мерзляк. Упражнения из учебника с ответами и решениями. Глава 1. НЕРАВЕНСТВА. § 5. Решение линейных неравенств с одной переменной. Числовые промежутки. Алгебра 9 Мерзляк Упражнения 110-141 + ОТВЕТЫ.