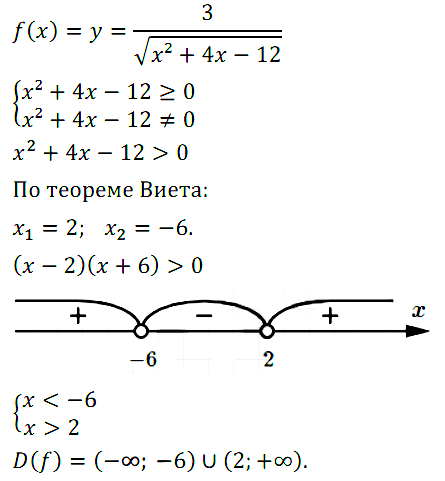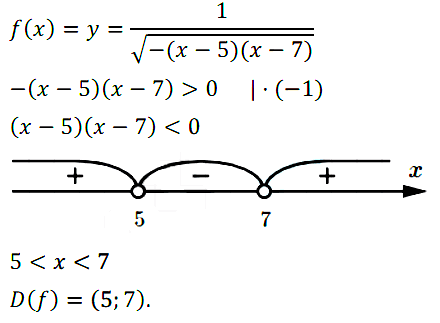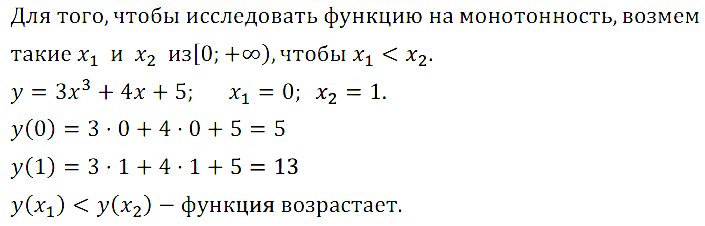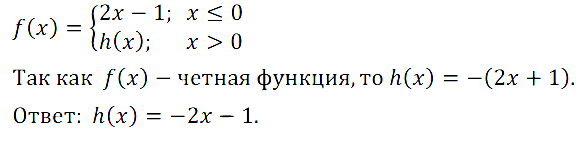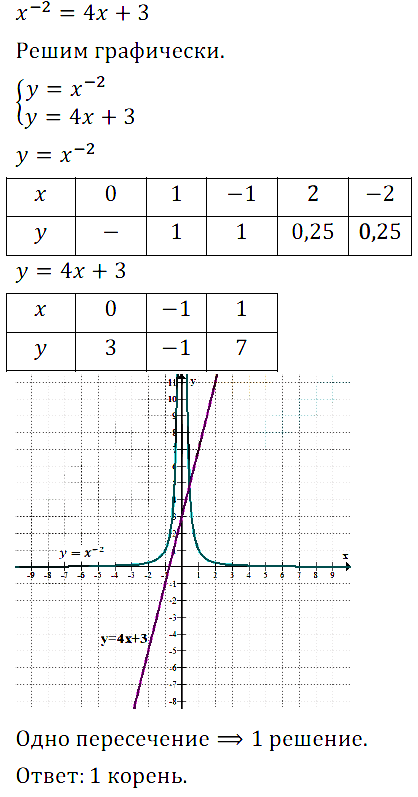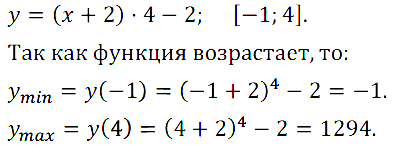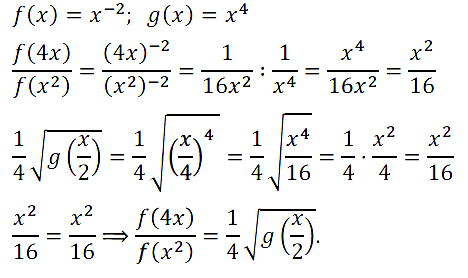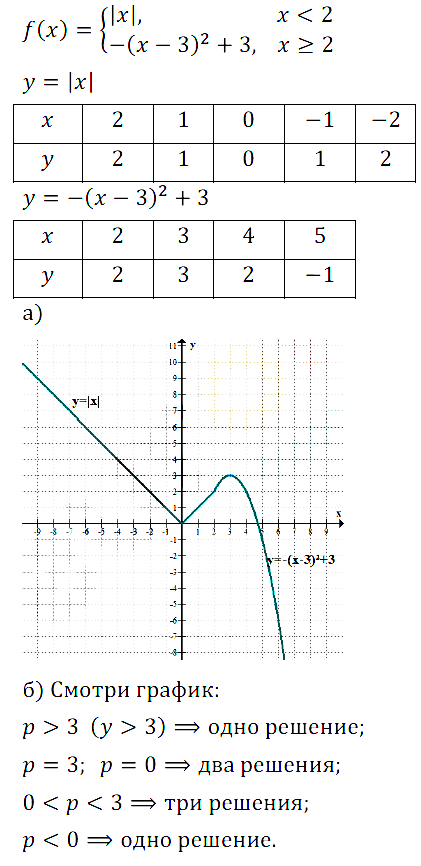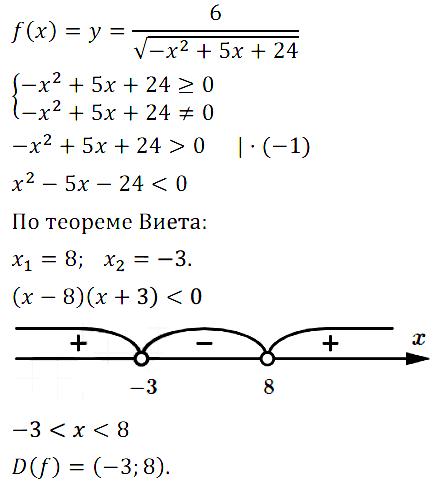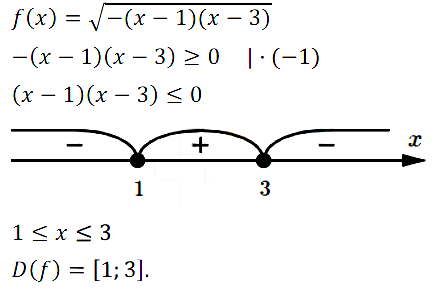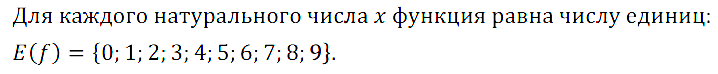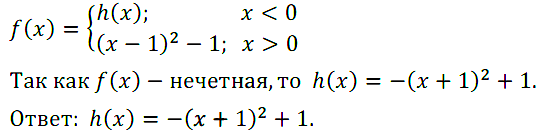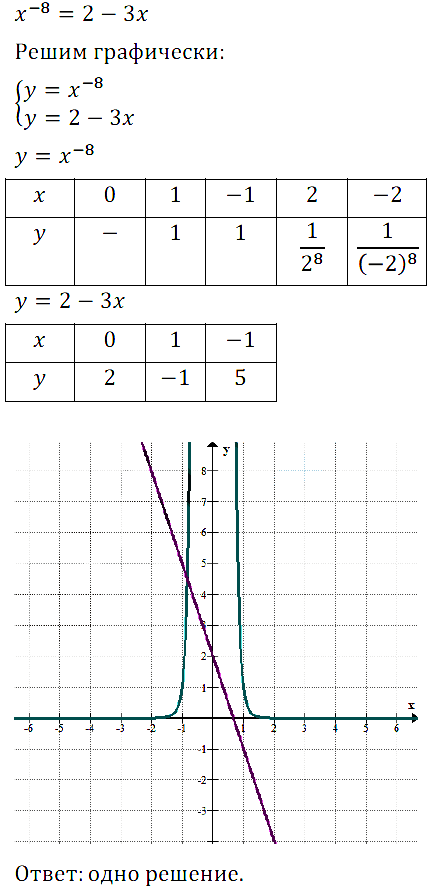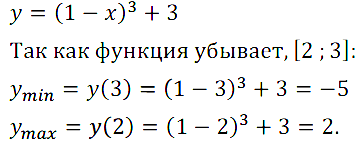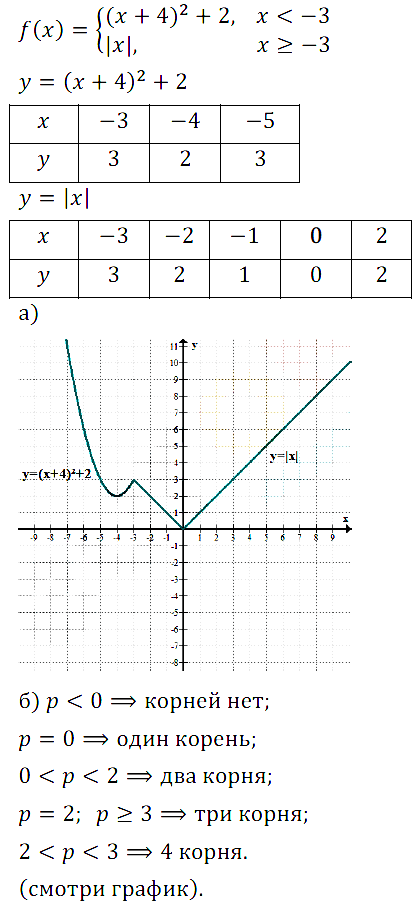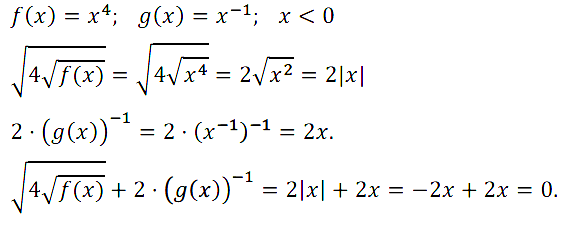Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). Домашняя контрольная работа № 3 с ответами и решениями (ГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИ).
ОГЛАВЛЕНИЕ Вернуться к списку тем учебника
Алгебра 9 класс (Мордкович)
Домашняя контрольная работа № 3
ДКР-3. Вариант 1
№ 1. Найдите область определения функции у = 3/√[x2 + 4x – 12].
№ 2. Придумайте аналитически заданную функцию у = f(х), для которой D(f) = (5; 7).
№ 3. Функция у = f(x) задана на множестве X всех двузначных натуральных чисел с помощью следующего правила: каждому числу х из X ставится в соответствие целая часть квадратного корня из числа х. Найдите область значений данной функции.
№ 4. Используя свойства числовых неравенств, исследуйте на монотонность функцию у = Зх3 + 4х + 5, х ∈ [0; +∞).
№ 5. Дана функция у = f(x), где f(x) = { 2x – 1, если х ≤ 0; { h(х), если х > 0.
Задайте h(x), если известно, что у = f(x) является чётной функцией.
№ 6. Определите число корней уравнения х–2 = 4х + 3.
№ 7. Найдите наименьшее и наибольшее значения функции у = (х + 2)4 – 2 на отрезке [–1, 4].
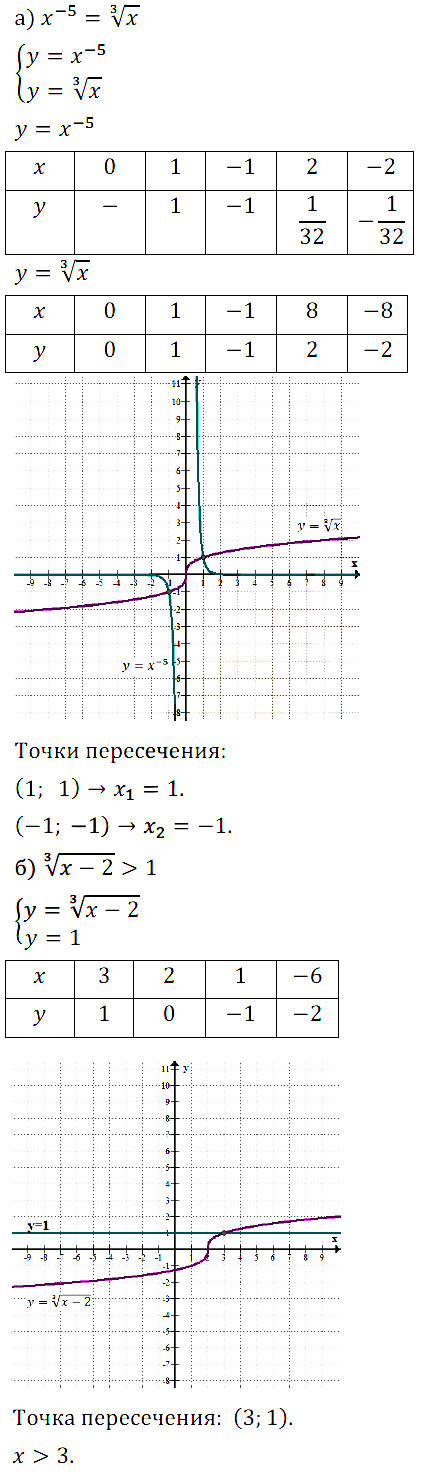
№ 8. Решите графически: а) уравнение x–5 = 3√x; б) неравенство 3√[x + 2] > 1.
№ 9. Даны функции у = f(х) и у = g(x), где f(х) = х–2, g(x) = х4. Докажите, что f(4x)/f(x2) = 1/4 • √[g(x/2)].
№ 10. Дана функция у = f(х), где f(х) = { |x|, если х < 2; { –(х – З)2 + 3, если х ≥ 2.
а) Постройте график функции у = f(х);
б) укажите число корней уравнения f(х) = р, где р — любое действительное число.
ДКР-3. Вариант 2
№ 1. Найдите область определения функции у = 6/√[–x2 + 5x + 24]
№ 2. Придумайте аналитически заданную функцию у = f(х), для которой D(f) = [1; 3].
№ 3. Функция у = f(х) задана на множестве всех натуральных чисел с помощью следующего правила: каждому числу х ставится в соответствие число единиц в записи куба числа х. Найдите область значений данной функции.
№ 4. Используя свойства числовых неравенств, исследуйте на монотонность функцию у = –х4 – x2 + 8, х ∈ [0; +∞).
№ 5. Дана функция у = f(х), где f(x) = { h(х), если х < 0; { (x – 1)2 – 1, если х > 0.
Задайте h(х), если известно, что у = f(x) является нечётной функцией.
№ 6. Определите число корней уравнения х–3 = 2 – 3х.
№ 7. Найдите наименьшее и наибольшее значения функции у = (1 – х)3 + 3 на отрезке [2; 3].
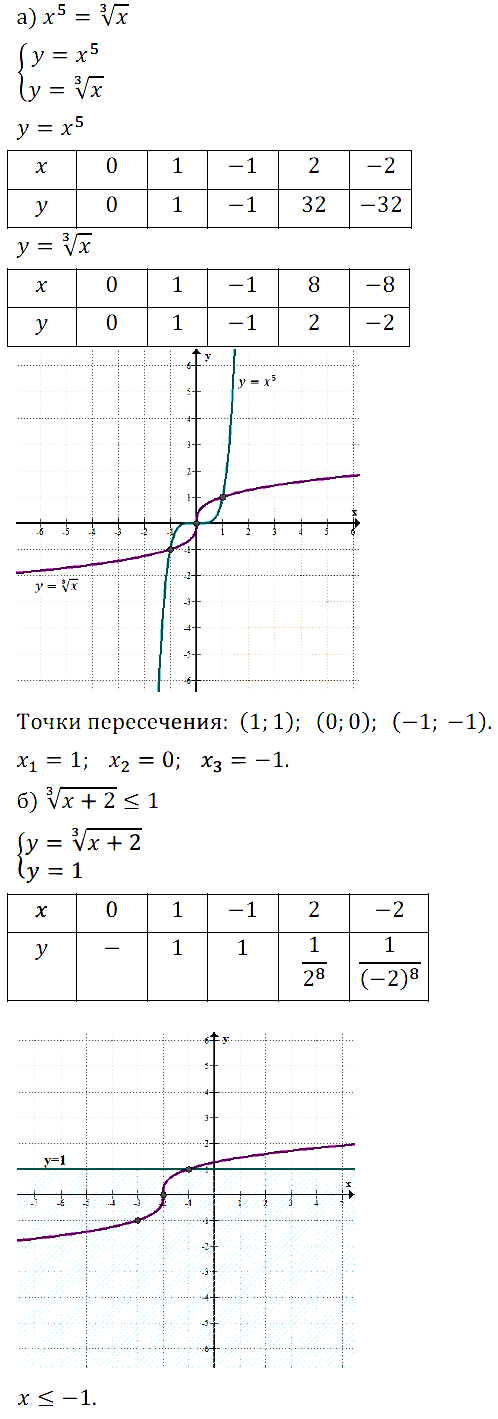
№ 8. Решите графически: а) уравнение х5 = 3√x; б) неравенство 3√[х + 2] ≤ 1.
№ 9. Даны функции у = f(х) и у = g(x), где f(х) = х4, g(x) = х–1. Докажите, что при х < 0 выполняется равенство √[ 4√[ f(x)]] + 2(g(x))–1 = 0.
№ 10. Дана функция у = f(х), где f(x) = { (x + 4)2 + 2, если х < –3; { |х|, если х ≥ –3.
а) Постройте график функции у = f(х);
б) укажите число корней уравнения f(х) = р, где р — любое действительное число.
Вы смотрели: ГДЗ Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИ. Домашняя контрольная работа № 3 с ответами и решениями