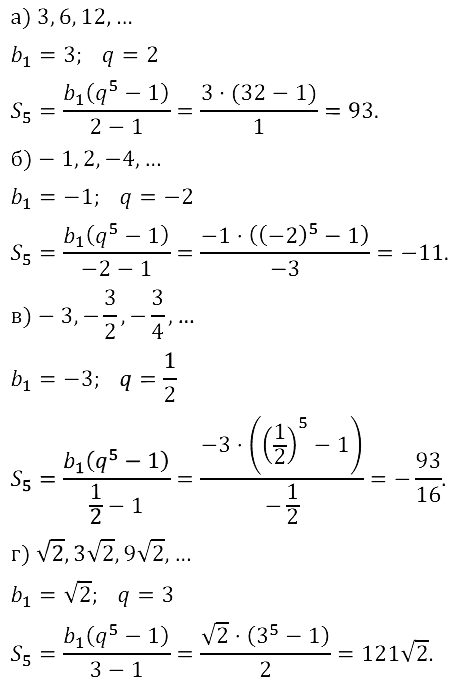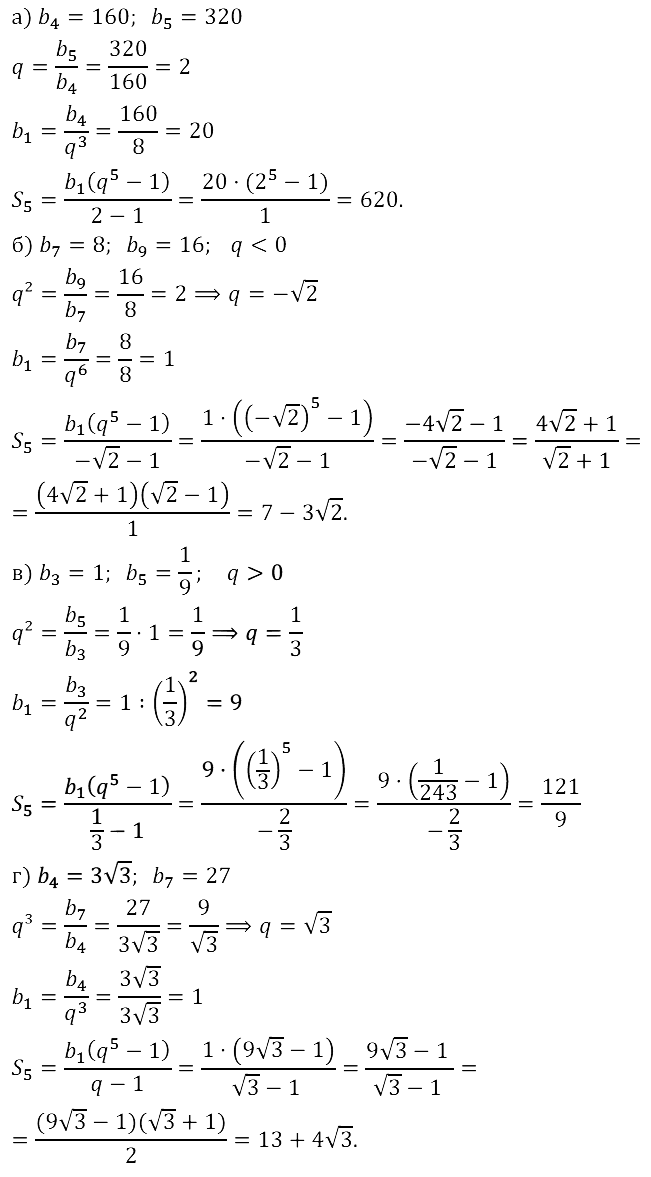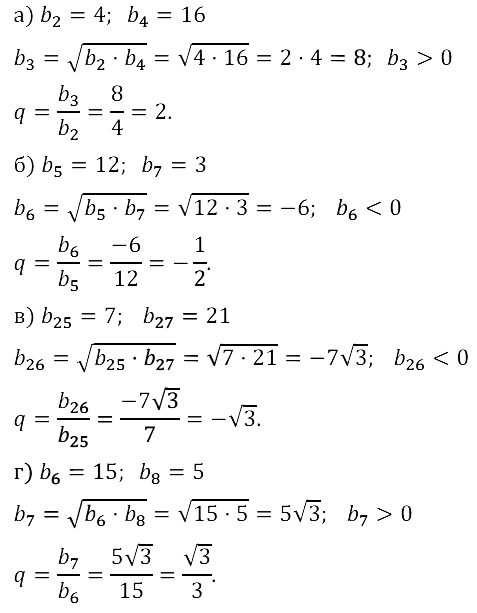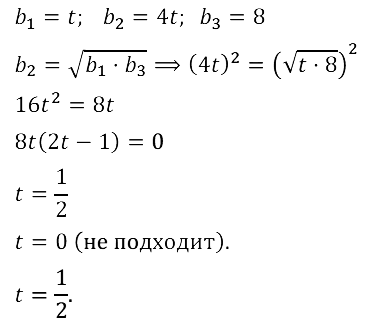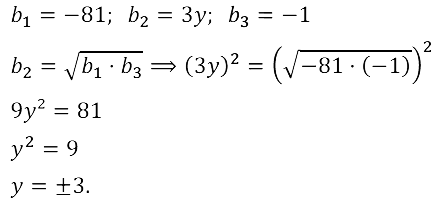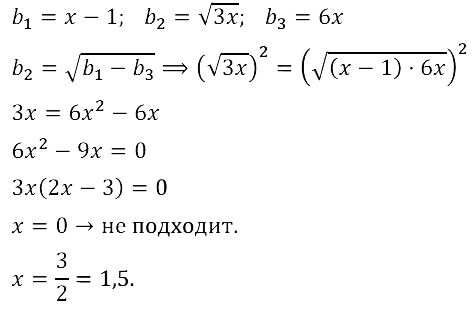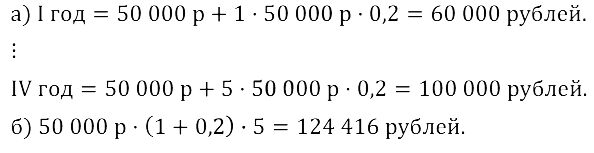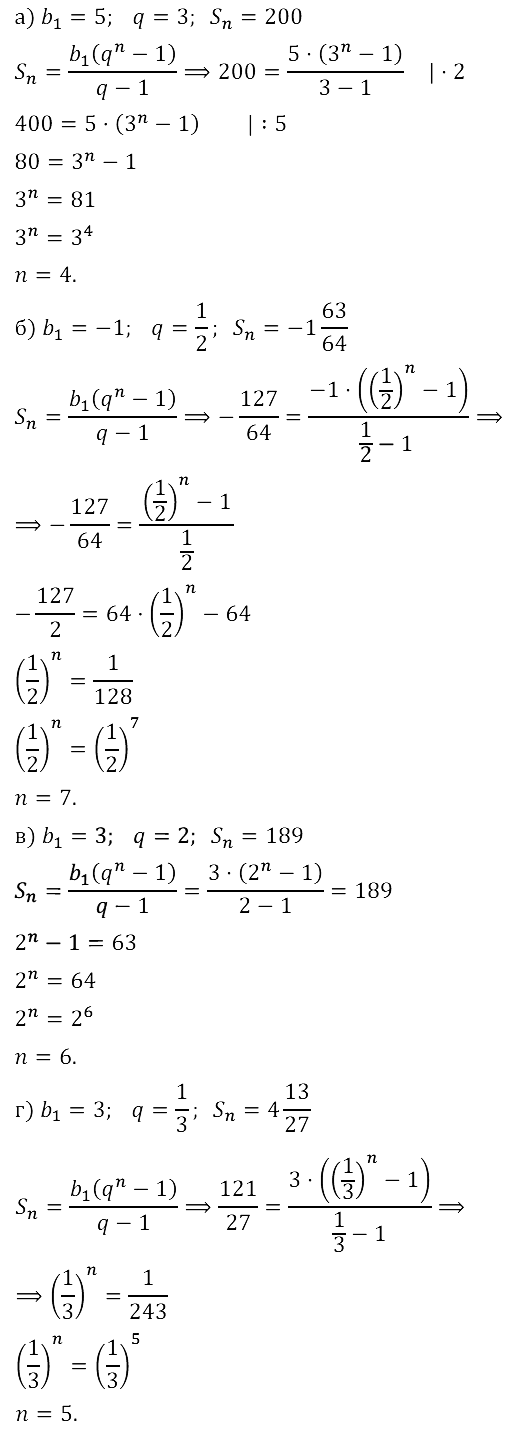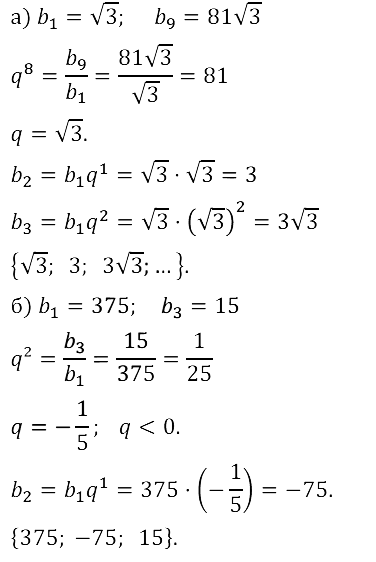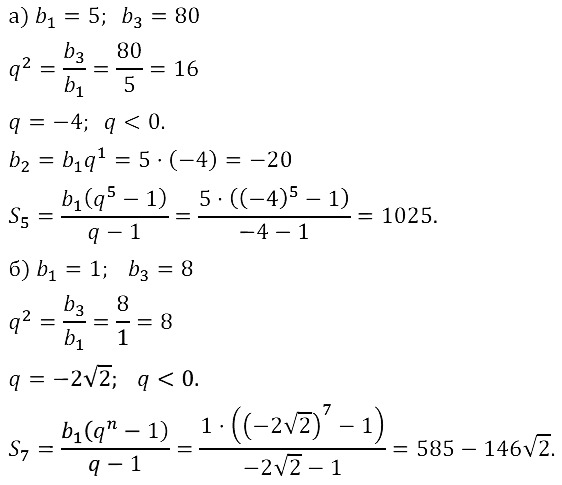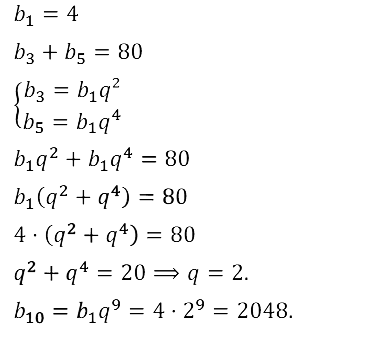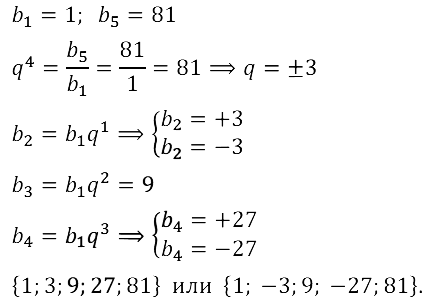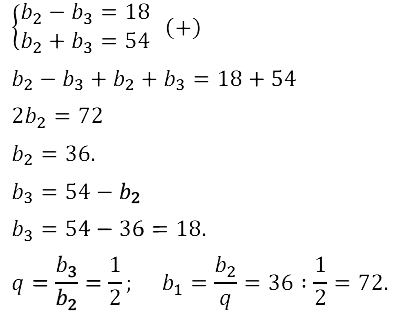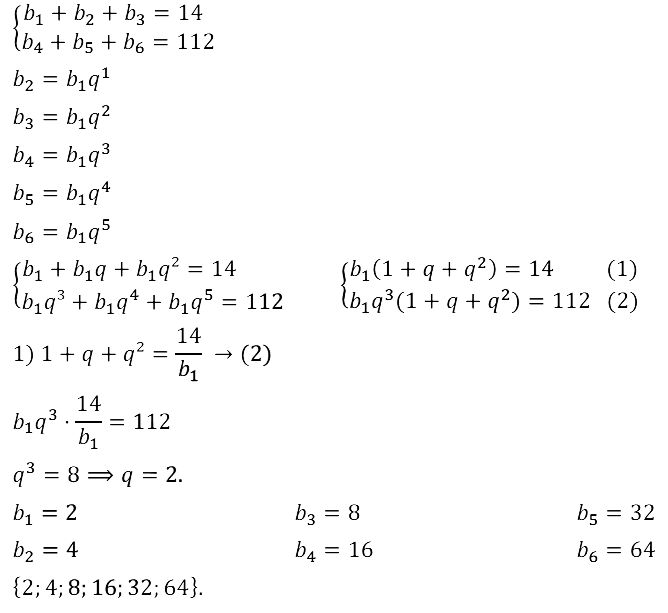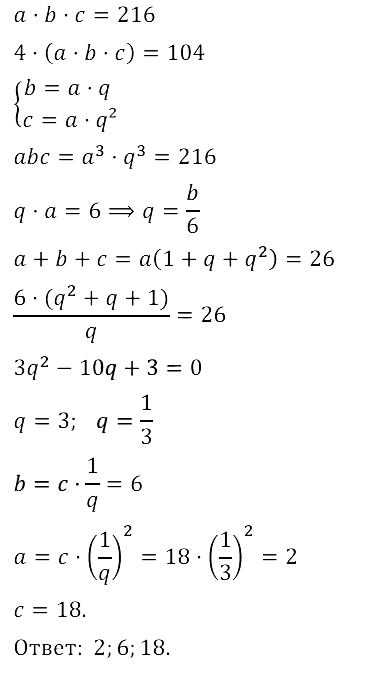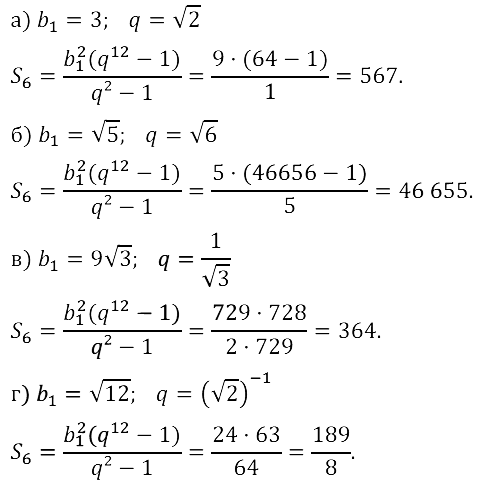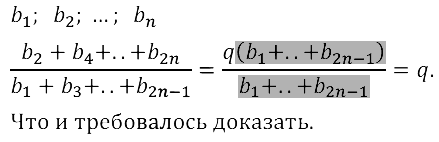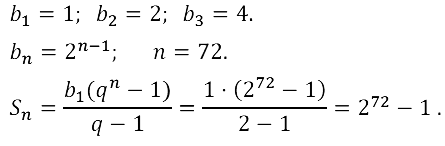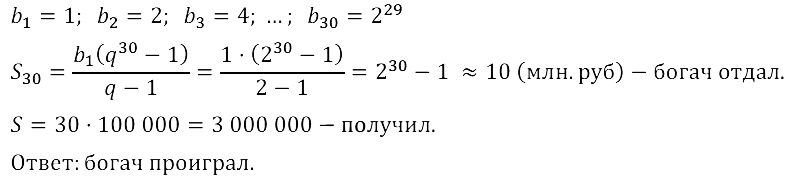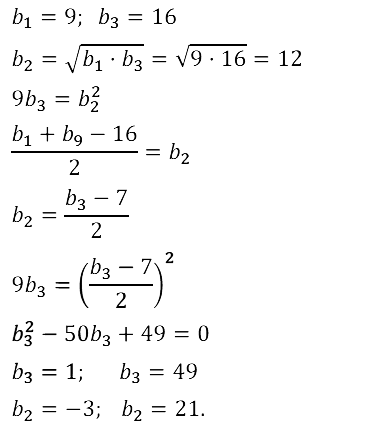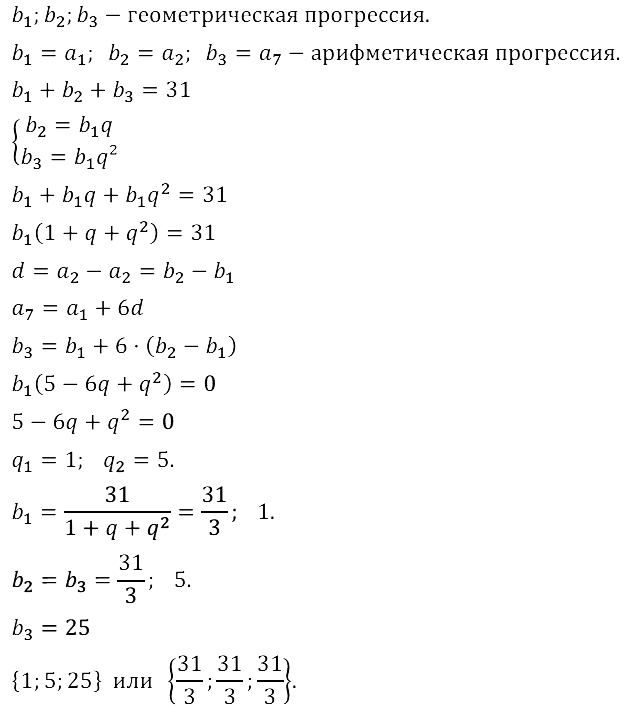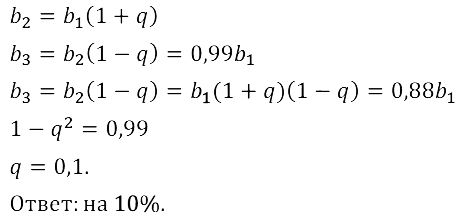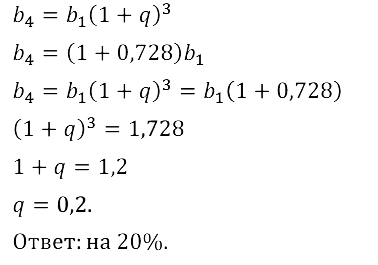Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2020-2023). ОТВЕТЫ на упражнения 17.28 — 17.58. § 17. Геометрическая прогрессия. ГЛАВА 4. ПРОГРЕССИИ.
ОГЛАВЛЕНИЕ Вернуться к списку тем учебника
Алгебра 9 класс (Мордкович)
Упражнения №№ 17.28 — 17.58
Нажмите на спойлер, чтобы посмотреть ответ на задание.
ГЛАВА 4. ПРОГРЕССИИ
§ 17. Геометрическая прогрессия
Задание № 17.28. Найдите сумму первых пяти членов геометрической прогрессии:
а) 3, 6, 12, …; б) –1, 2, –4, …; в) –3, –3/2, –3/4, …; г) √2, 3√2, 9√2, … .
Задание № 17.29. Найдите S5 для геометрической прогрессии (bn), если:
а) b4 = 160, b5 = 320; б) b7 = 8, b9 = 16 (q < 0); в) b3 = 1, b5 = 1/9 • (q > 0); г) b4 = 3√3, b7 = 27.
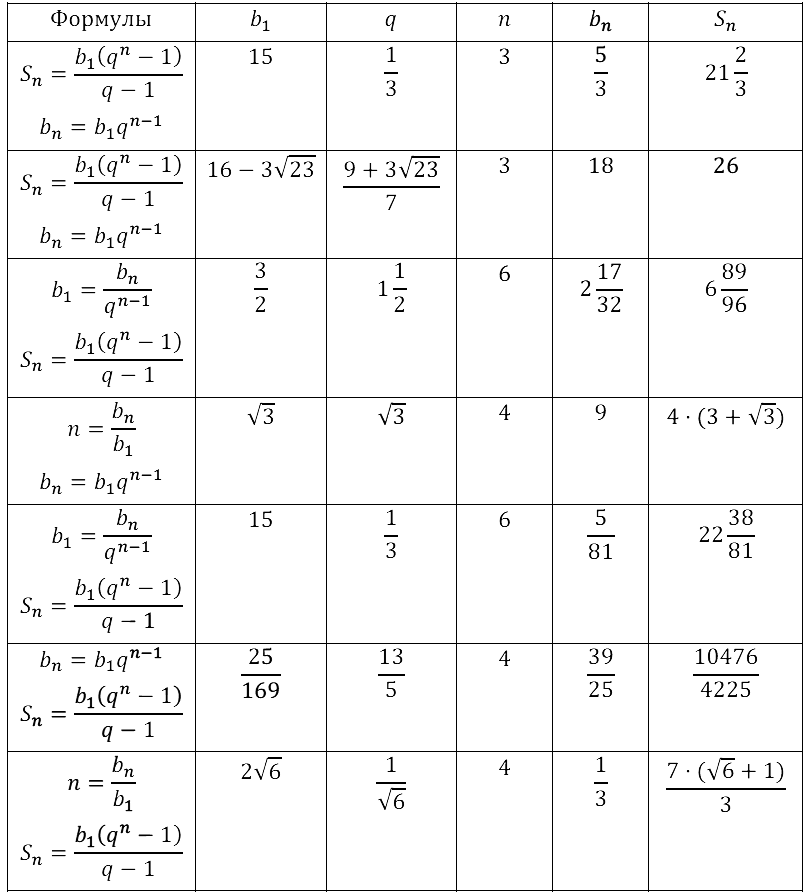
Задание № 17.30.
Задание № 17.31.
Задание № 17.32. Найдите те значения переменной t, при которых числа t, 4t, 8 являются последовательными членами геометрической прогрессии.
Задание № 17.33. Найдите те значения переменной у, при которых числа –81, 3у, –1 являются последовательными членами геометрической прогрессии.
Задание № 17.34. Найдите те значения переменной х, при которых числа х – 1, √Зх, 6х являются последовательными членами геометрической прогрессии.
Задание № 17.35. Клиент взял в банке кредит в размере 50 000 евро на 5 лет под 20 % годовых. Какую сумму он в итоге выплатит, если условия погашения кредита таковы:
а) проценты возвращаются в банк ежегодно;
б) весь кредит с процентами возвращается в банк в конце срока?
Задание № 17.36.
Задание № 17.37.
Задание № 17.38.
Задание № 17.39.
Задание № 17.40. а) Дана возрастающая геометрическая прогрессия (bn). Найдите знаменатель и первые три члена этой прогрессии, если b1 = √3, b9 = 81√3.
б) Дана убывающая геометрическая прогрессия (bn). Найдите знаменатель и первые три члена этой прогрессии, если b1 = 375, b3 = 15.
Задание № 17.41. а) Дана знакочередующаяся геометрическая прогрессия (bn). Найдите знаменатель прогрессии и сумму её первых пяти членов, если b1 = 5, b3 = 80.
б) Дана знакочередующаяся геометрическая прогрессия (bn). Найдите знаменатель прогрессии и сумму её первых семи членов, если b1 = 1, b3 = 8.
Задание № 17.42. Первый член возрастающей геометрической прогрессии (bn) равен 4, а сумма третьего и пятого членов равна 80. Найдите q и b10, если известно, что прогрессия возрастающая.
Задание № 17.43. Между числами 1 и 81 вставьте три таких числа, чтобы они вместе с данными числами образовали геометрическую прогрессию.
Задание № 17.44.Разность между вторым и третьим членами геометрической прогрессии равна 18, а их сумма 54. Определите первый член и знаменатель прогрессии.
Задание № 17.45. Составьте конечную геометрическую прогрессию из шести членов, зная, что сумма трёх первых членов равна 14, а трёх последних 112.
Задание № 17.46. Длина, ширина и высота прямоугольного параллелепипеда образуют геометрическую прогрессию. Объём параллелепипеда равен 216 м3, а сумма длин всех его ребёр равна 104 м. Найдите измерения параллелепипеда.
Задание № 17.47.
Задание № 17.48.
Задание № 17.49.
Задание № 17.50. Докажите, что в конечной геометрической прогрессии, имеющей чётное число членов, отношение суммы членов, стоящих на чётных местах, к сумме членов, стоящих на нечётных местах, равно знаменателю прогрессии.
Задание № 17.51. Бактерия, попав в живой организм, к концу 20–й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т. д. Найдите число бактерий, образующихся из одной бактерии к концу суток.
Задание № 17.52. Однажды богач заключил выгодную, как ему казалось, сделку с человеком, который целый месяц ежедневно должен был приносить по 100 тыс. р., а взамен в первый день месяца богач должен был отдать 1 к., во второй — 2 к., в третий — 4 к., в четвёртый — 8 к. и т. д. в течение 30 дней. Сколько денег получил богач и сколько он отдал? Кто выиграл от этой сделки?
Задание № 17.53. Три числа составляют конечную геометрическую прогрессию. Если последнее число уменьшить на 16, то получится конечная арифметическая прогрессия. Найдите два последних числа, если первое равно 9.
Задание № 17.54. Сумма трёх чисел, составляющих конечную арифметическую прогрессию, равна 24. Если второе число увеличить на 1, а последнее на 14, то получится конечная геометрическая прогрессия. Найдите эти числа.
Задание № 17.55. Сумма первых трёх членов геометрической прогрессии равна 91. Если к этим числам прибавить соответственно 25, 27 и 1, то получатся три числа, являющиеся последовательными членами некоторой арифметической прогрессии. Найдите седьмой член исходной геометрической прогрессии, если известно, что он меньше 1000.
Задание № 17.56. Три числа, сумма которых равна 31, можно рассматривать как три последовательных члена некоторой геометрической прогрессии или как первый, второй, седьмой члены некоторой арифметической прогрессии. Найдите эти числа.
Задание № 17.57. На биржевых торгах в понедельник вечером цена акции банка «Городской» повысилась на некоторое количество процентов, а во вторник произошло снижение стоимости акции на то же число процентов. В результате во вторник вечером цена акции составила 99 % от её первоначальной цены в понедельник утром. На сколько процентов менялась котировка акции в понедельник и во вторник?
Задание № 17.58. В результате трёхкратного повышения цены на некоторый товар на одно и то же число процентов цена товара стала превышать первоначальную цену на 72,8%. На сколько процентов повышалась цена на товар каждый раз?
Вы смотрели: ГДЗ Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович. ГЛАВА 4. ПРОГРЕССИИ. § 17. Геометрическая прогрессия. ОТВЕТЫ на задачи 17.28 — 17.58.