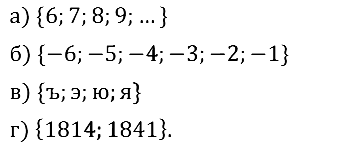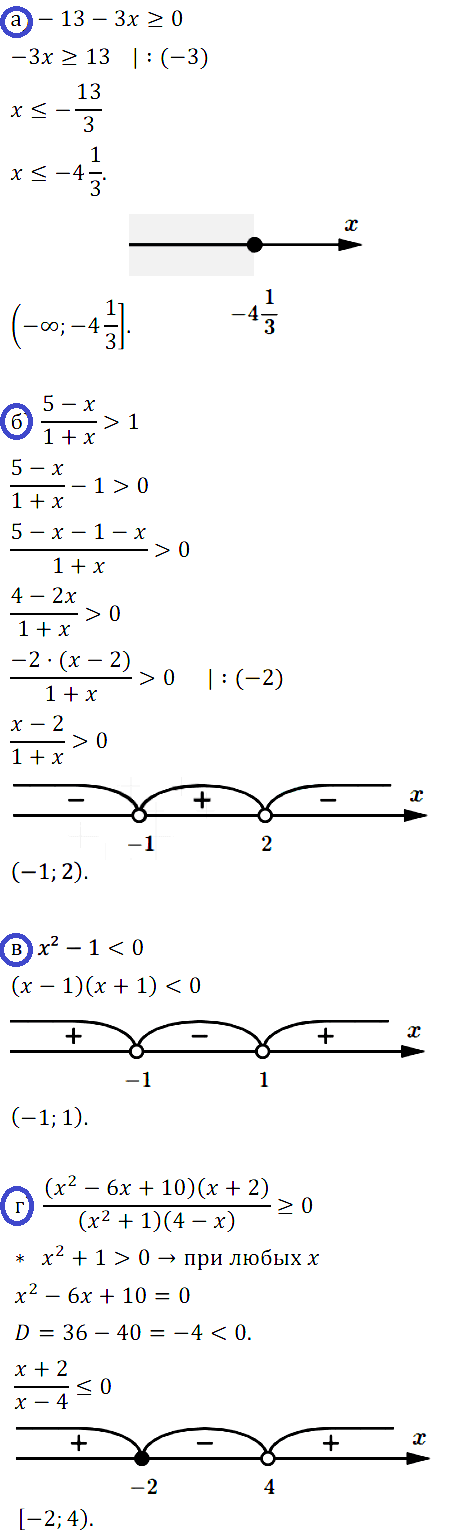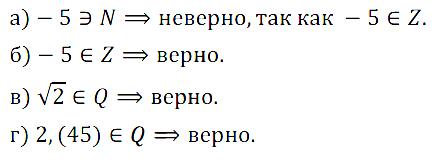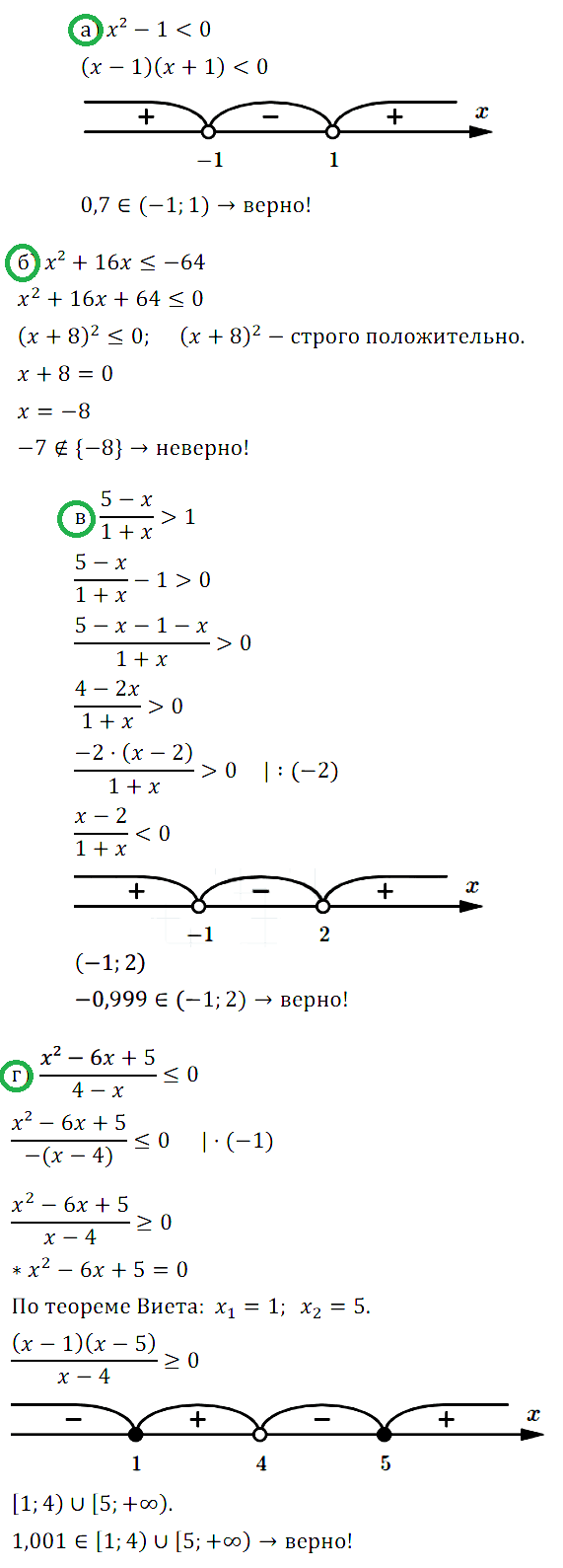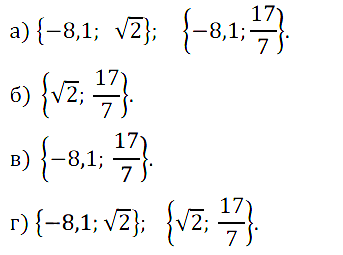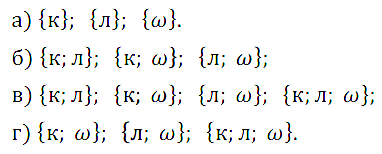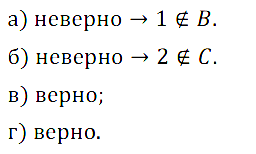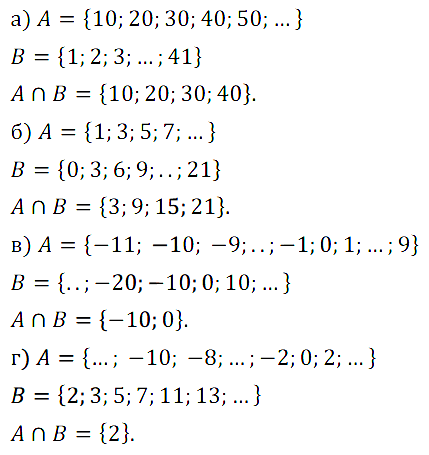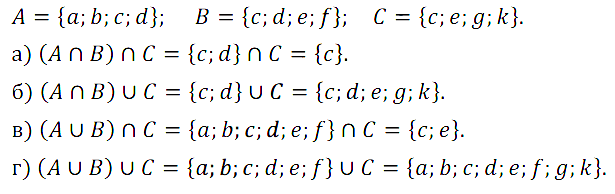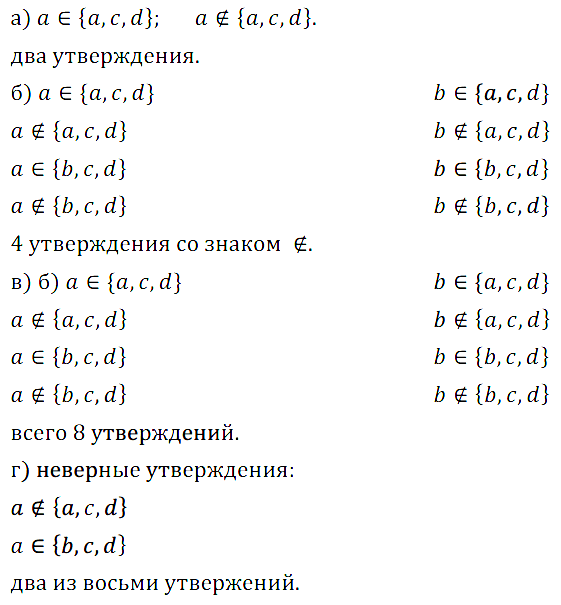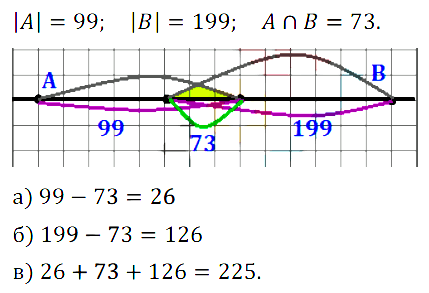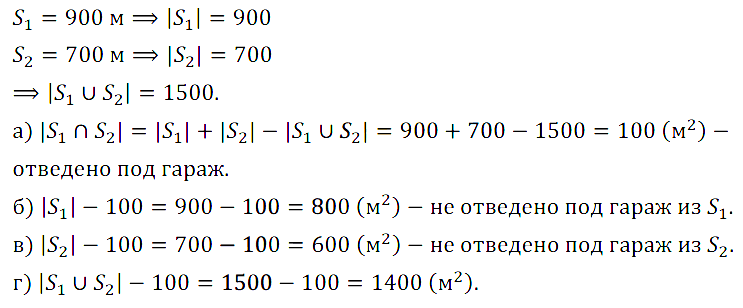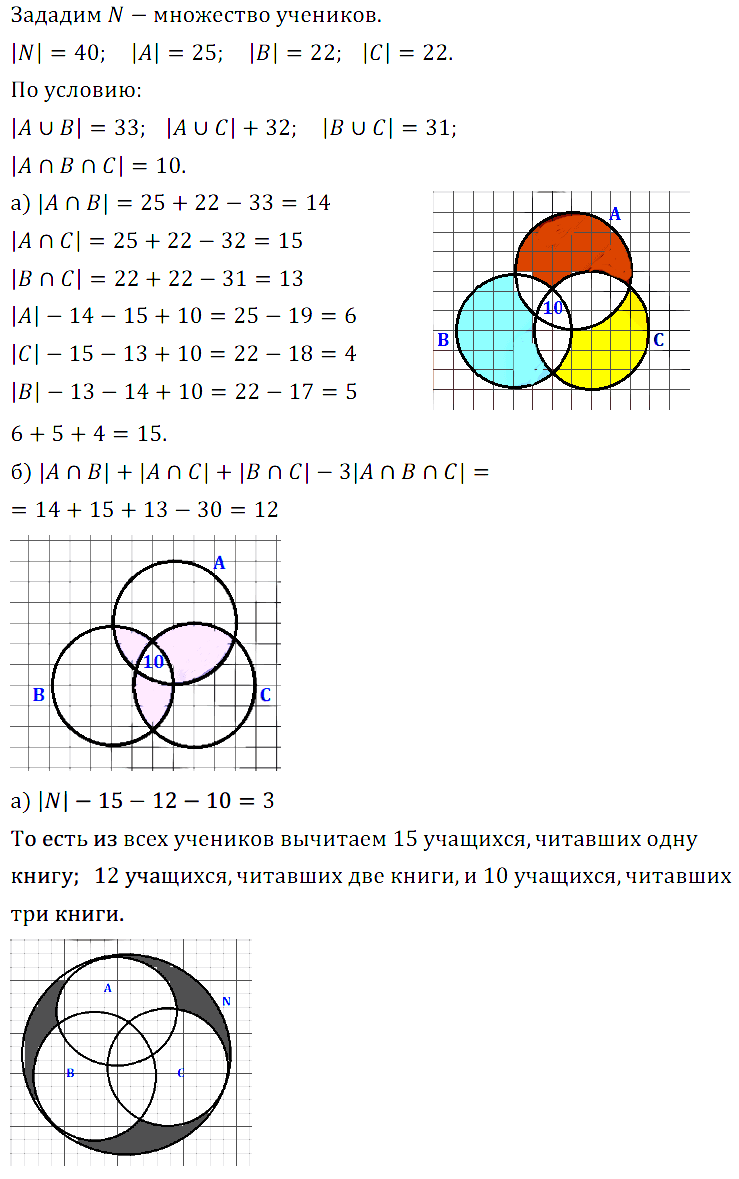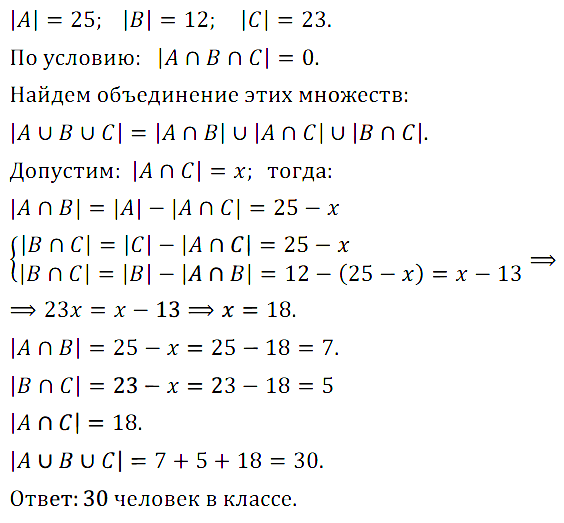Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ОТВЕТЫ на упражнения 3.1 — 3.25. § 3. Множества и операции над ними (РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА И ИХ СИСТЕМЫ).
ОГЛАВЛЕНИЕ Вернуться к списку тем учебника
Алгебра 9 класс (Мордкович)
Упражнения №№ 3.1 — 3.25
Нажмите на спойлер, чтобы посмотреть ответ на задание.
§ 3. Множества и операции над ними
Задание № 3.1. Множество задано словесным описанием. Задайте это множество, перечислив его элементы:
а) цифры, которые больше 5;
б) целые отрицательные числа, которые больше –7;
в) четыре последние буквы русского алфавита;
г) различные цифры года рождения и года гибели М. Ю. Лермонтова.
Задание № 3.2. Множество задано перечислением своих элементов. Приведите какое–нибудь его словесное описание:
а) {0, 2, 4, 6, 8}; в) {3, 6, 9, …, 27, 30};
б) {2, 3, 5, 7}; г) {А, В, С, D, …, X, У, Z).
Задание № 3.3. Запишите заданное множество в виде числового промежутка:
а) {х | – 13 – 3х ≥ 0}; в) {х | х2 – 1 < 0};
б) {x | (5 – x)/(1 + x) > 1}; г) {x | (х2 – 6х + 10)(х + 2)/((x2 + 1)(4 – x)) ≥ 0}
Задание № 3.4. Верно ли, что:
а) –5 ∈ N; б) –5 ∈ Z; в) √2 ∈ Q; г) 2,(45) ∈ Q?
Задание № 3.5. Докажите, что заданное множество состоит из одного числа (элемента), и найдите это число:
а) {х | х2 ≤ 0}; в) {х | 41√х ≤ 0}; …
Задание № 3.6. Верно ли, что: а) 0,7 ∈ {х | х2 – 1 < 0}; б) –7 ∈ {х | х2 + 16х ≤ –64}; …
Задание № 3.7. а) Решите уравнение х(х2 + 19) + 6 = (2х + 3)(3х + 2) – х2.
б) Запишите множество М корней этого уравнения, перечислив его элементы в порядке возрастания.
в) Запишите все возможные способы перечисления элементов множества М.
г) Сколько всего имеется способов перечисления элементов множества M?
Задание № 3.8 Дано множество {–8,1; √2; 17/7}. Перечислите все его подмножества, состоящие из двух чисех:
а) разного знака; б) положительных; в) рациональных; г) среди которых есть иррациональное число.
Задание № 3.9 Дано множество А = {к, л, w}. Перечислите все его подмножества, состоящие:
а) из одного элемента;
б) из двух элементов;
в) более чем из одного элемента;
г) из элементов, среди которых есть буквы как русского, так и латинского алфавита.
Задание № 3.10.
Задание № 3.11.
Задание № 3.12.
Задание № 3.13.
Задание № 3.14.
Задание № 3.15.
Задание № 3.16. а) Найдите все натуральные числа, кубы которых — трёхзначные числа;
б) запишите множество М таких трёхзначных чисел, перечислив их в порядке убывания;
в) запишите множество А последних цифр элементов множества М, перечислив их в порядке возрастания;
г) сколькими способами можно перечислить различные между собой вторые цифры чисел из множества M?
Задание № 3.17. Запишите заданное множество в виде числового промежутка:
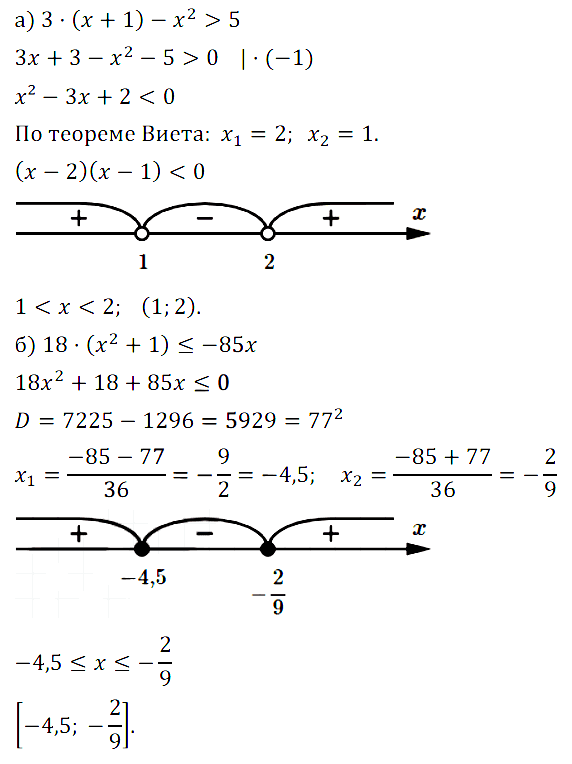
а) {х | 3(х + 1) – х2 > 5}; б) {х | 18(x2 + 1) < –85x}.
Задание № 3.18. В записи «* ∈ {4, Δ, 9}» вместо значков * и Δ можно поставить любые цифры, меньшие 3. Будут получаться различные утверждения: 0 ∈ {4, 0, 9}, 1 ∈ {4, 2, 9} и т. п.
а) Сколько получится утверждений, в которых на первом месте стоит цифра 2?
б) Сколько получится утверждений, в которых на месте А стоит положительная цифра?
в) Сколько всего утверждений получится?
г) Какую часть из всех утверждений составляют верные утверждения?
Задание № 3.19 Известно, что а, b, с, d — попарно различные числа. В записи «* □ {Δ, с, d}» на места * и Δ можно поставить числа а или b, а на место □ можно поставить знак ∈ или знак ∉. Будут получаться различные утверждения.
а) Сколько получится утверждений, в которых нет числа b?
б) Сколько получится утверждений, в которых использован знак ∉?
в) Сколько всего утверждений получится?
г) Какую часть из всех утверждений составляют неверные утверждения, начинающиеся с числа а?
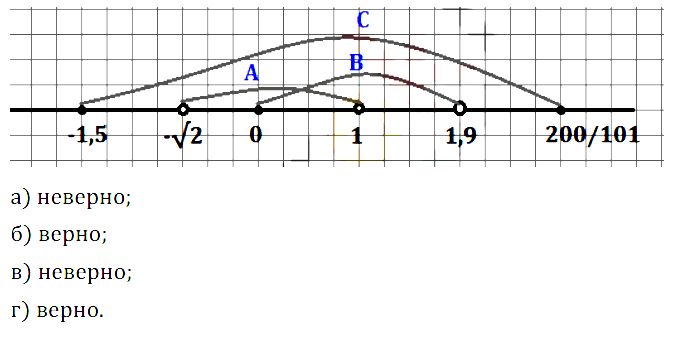
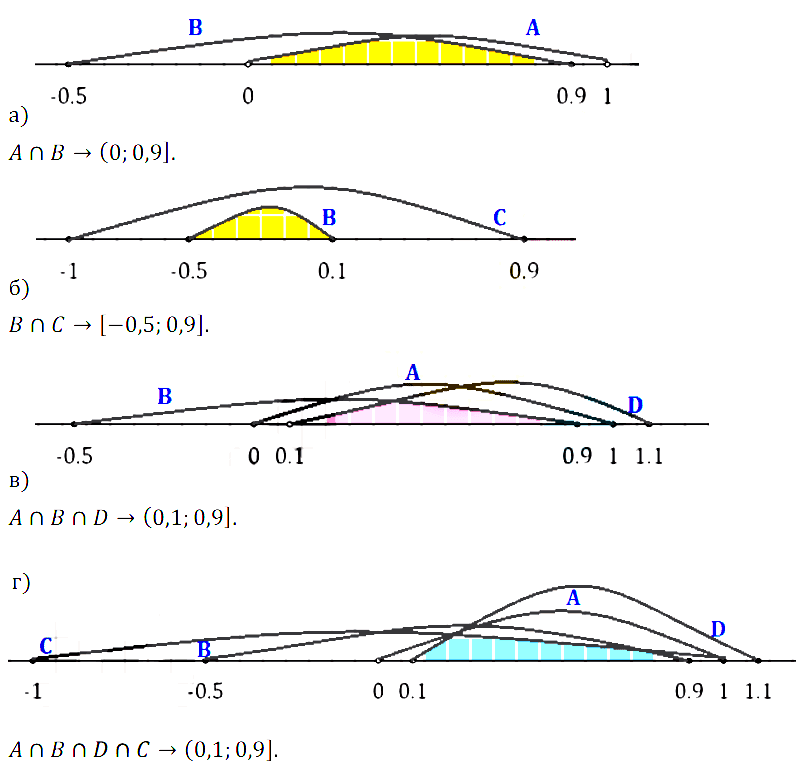
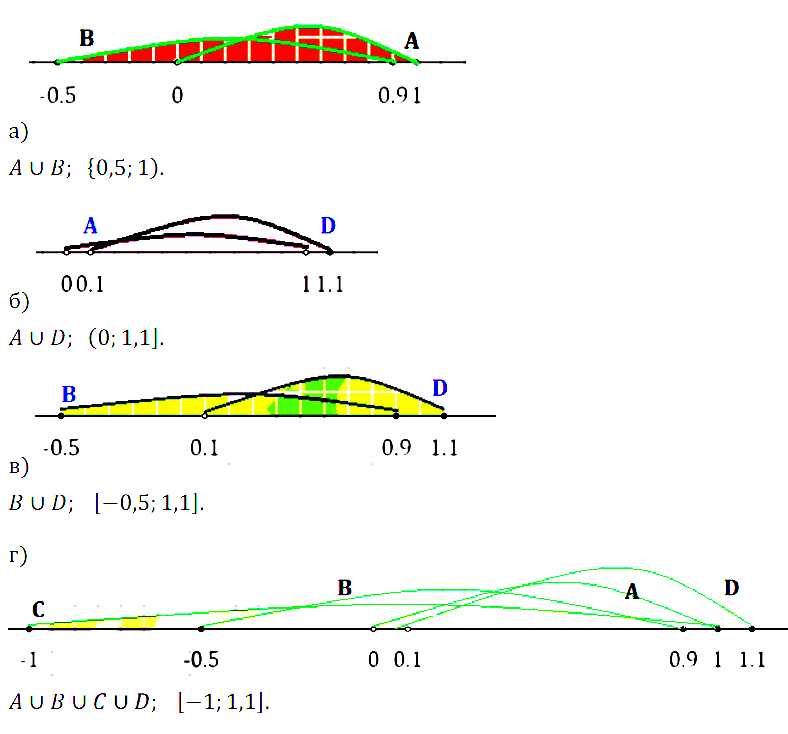
Задание № 3.20. Даны три числовых промежутка:
А = (7,7; 11), В = [√97; √167], С = (√101; 13]. Найдите множества:
а) (А ∩ В) ∩ С; в) (А ∪ В) ∩ С;
б) (А ∩ В) ∪ С; г) (А ∪ B) ∪ С.
Решите задачи, используя круги (диаграммы) Эйлера:
Задание № 3.21. Множество А состоит из 99 элементов, множество В — из 199 элементов, а множество А ∩ В — из 73 элементов. Сколько элементов:
а) принадлежит множеству А, но не принадлежит множеству В;
б) принадлежит множеству В, но не принадлежит множеству А;
в) принадлежит множеству А ∪ В?
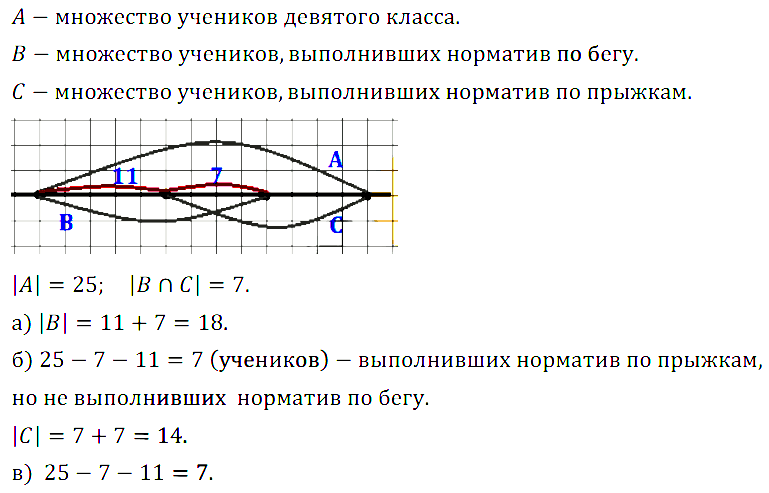
Задание № 3.22 На школьной спартакиаде каждый из 25 учеников 9–го класса выполнил норматив или по бегу, или по прыжкам в высоту. Оба норматива выполнили 7 учеников, a 11 учеников выполнили норматив по бегу, но не выполнили норматив по прыжкам в высоту. Сколько учеников выполнили норматив: а) по бегу; б) по прыжкам в высоту; в) по прыжкам в высоту при условии, что не выполнен норматив по бегу?
Задание № 3.23 По плану застройки участок площадью 1500 м2 состоит из двух пересекающихся прямоугольников, их пересечение отведено под гараж. Площадь первого прямоугольника равна 900 м2, площадь второго — 700 м2. Найдите площадь: а) участка, отведённого под гараж; б) части первого прямоугольника, не отведённого под гараж; в) части второго прямоугольника, не отведённого под гараж; г) части застройки без учёта гаража.
Задание № 3.24 На уроке литературы учитель решил узнать, кто из 40 учеников 9-го класса читал книги А, В, С. Результаты опроса выглядят так: книгу А прочитали 25 учеников, книгу В — 22 ученика, книгу С — 22 ученика; одну из книг (А или В) прочитали 33 ученика, одну из книг (А или С) прочитали 32 ученика, одну из книг (В или С) — 31 ученик. Все три книги прочитали 10 учеников. Сколько учеников: а) прочитали только по одной книге; б) прочитали ровно две книги; в) не читали ни одной из указанных книг?
Задание № 3.25 Каждый из учеников 9-го класса в зимние каникулы ровно два раза был в театре, посмотрев спектакли А, В или С. При этом спектакли А, В, С видели соответственно 25, 12 и 23 ученика. Сколько учеников в классе?
Вы смотрели: Алгебра 9 класс. Часть 2 (Задачник) УМК Мордкович (2019-2021). ГЛАВА 1. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА И ИХ СИСТЕМЫ. § 3. Множества и операции над ними. ОТВЕТЫ на задачи 3.1 — 3.25.